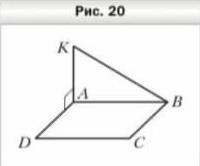
На рисунке 20 изображён прямоугольник ABCD. Через вершину A проведена прямая AK, которая перпендикулярна прямой AD. Докажите, что прямая AD перпендикулярна плоскости AKB

Признак перпендикулярности прямой и плоскости:

если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то эта прямая перпендикулярна плоскости.

Две прямые лежат в плоскости и пересекаются:

AK⊂(AKB);  AB⊂(AKB);  AK∩AB=A.

Прямая AD перпендикулярна двум пересекающимся прямым, лежащим  в плоскости:

AD⊥AK - по условию;  AD⊥AB  - по прямоугольнику ABCD;

Следовательно, прямая AD перпендикулярна плоскости (AKB):

⇒   AD⊥(AKB).