Предмет: Алгебра
Автор: Полинка1111
Вопрос задан 10 лет назад

Докажите,что функция спадает на всем промежутке.Нужно найти производную,область значений х....основное тригонометрическое тождество,сказали,что не подходит,не зн,что делать теперь....

Приложения:

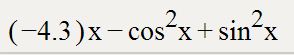
Ответы

Ответ дал: bearcab

Возьмем первую производную

$f'(x)=-4,3-2cos(x)*(-sin(x))+2sin(x)*cos(x)=$

$=-4,3+2sin(x)cos(x)+2sin(x)cos(x)=-4,3+4sin(x)cos(x)=$

Воспользуемся тождеством

2sin(a)cos(a)=sin(2a).

$=-4,3+2sin(2x)=$ .

То есть $f'(x)=-4,3+2sin(2x)$ .

Заметим, что самое большое значение, которое может принимать sin(2x) - это 1. Даже при этом значении -4,3+2*1=-2,3<0. При остальных значениях функции значение производной будет еще меньше. То есть значение производной всегда будет меньше нуля при любом х. Значит функция на протяжении всей своей области определения $xin(-infty;infty)$ - убывает.