• Предмет: Алгебра
  • Автор: soganesan410
  • Вопрос задан 2 года назад
< >

Найти область определения y=кореньx^2-15x+14​

ofhfjfhcyfhs: Сколько тебе лет?
soganesan410: 16

Ответы

Ответ дал: Техномозг
0

Область определения функции - это множество всех значений, которые может принимать её аргумент (аргумент - это "x").

Решение:

y = \sqrt{(x^2-15x+14)}

D(f): x^2-14x+15 \geq 0  

x^2-15x+14 = 0 \\ \\D = (-15)^2-4\cdot1\cdot14 = 169 = 13^2 \\ \\ x_1 = \dfrac{-b+\sqrt{D}}{2a} = \dfrac{15+13}{2} = 14\\\\x_2 = \dfrac{-b-\sqrt{D}}{2a} = \dfrac{15-13}{2} = 1

Ответ: D(f) = (-∞;1] ∪ [14;+∞)

Приложения:
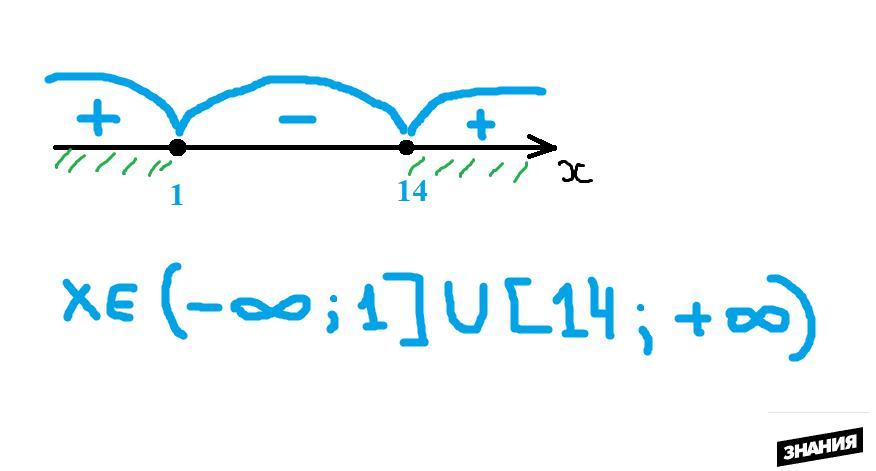
Техномозг: Удачи!
Техномозг: Обратите внимание - точка "0" закрашена, скобочка квадратная, так как нуль тоже входит в промежуток области определениях
Техномозг: определения*
Похожие вопросы
Английский язык
1 год назад
решите пожалуйста 1,2,3,4. 4 сколько увидите ​
Русский язык
1 год назад
Подберите указательное местоимение которое должно стоять на месте пропуска в предложении 3 )На иллюстрациях к сказкам можно увидеть стилизованный образ рыбы-кита с огромной выпуклой головой и
Русский язык
2 года назад
Понаблюдай, как по-разному можно сравнить одуванчик с солнцем.
Математика
2 года назад
Запишите дроби в виде процентов: 0.5 0,4 0,15 1,25 2,35 0,36
География
7 лет назад
ПОДСКАЖИТЕ ПОЖАЛУЙСТА КАК РЕШИТЬ! Я НЕ ПОНИМАЮ​
Математика
7 лет назад
Масса Алёши и Толи - 61 кг, Толи и Вити -68 кг, А Вити и Алёши-75 кг Какова масса каждого мальчика
Алгебра
9 лет назад
Б и г, пожалуйста. Хочу свериться.
Математика
9 лет назад
скорость течения реки 5 км час теплоход проплыл по течению 240 км в час за 8 часов.какое время необходимо затратить ему на обратный путь.если собственная скорость не изменилась