Помогите пожалуйста.
Abcd-ромб,
sc перпендикулярно abc,
ab=10,bd=12,sc=15.
Определить вид треугольников:sco,sob
Найти:ac,so,sb,sa
Рисунок к задаче не ишел

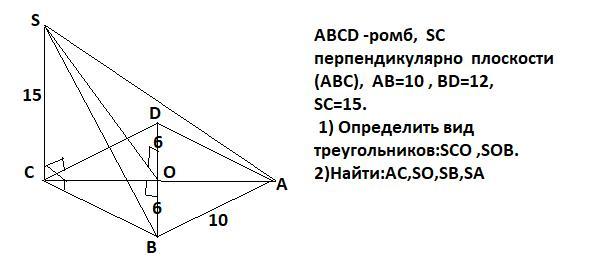
ABCD -ромб,  SC перпендикулярно  плоскости (АВС),  АВ=10 , ВD=12, SC=15. 1) Определить вид треугольников:SCO ,SOB. 2)Найти:AC,SO,SB,SA

Объяснение:

1) Т.к.  SC ⊥ (АВС), то SC  перпендикулярна любой прямой , лежащей в этой плоскости ⇒ SC ⊥ СО , поэтому ΔSCO- прямоугольный.

По свойству диагоналей ромба СА⊥BD . Тогда по т. о трех перпендикулярах : если проекция СО⊥ОВ ( прямой , лежащей в плоскости), то и наклонная SO⊥OB ⇒ΔSOB -прямоугольный.

2)По свойству диагоналей ромба : ∠ВОА=90° и ВО=12:2=6

ΔВОА прямоугольный , по т. Пифагора ОА=√(10²-6²)=8 ⇒ АС=2*8=16 .

ΔSCO-прямоугольный  ,CO=OA=8 , по т. Пифагора SO=√(15²+8²)=17 .

ΔSOB-прямоугольный  ,по т. Пифагора SB=√(17²+6²)=√325=5√13 .

ΔSCA-прямоугольный  ,по т. Пифагора SB=√(15²+16²)=√481.