Из точки K проведены две наклонные, равные 17см и 15см. Проекция одной из них на 4см больше проекции другой. Найдите проекции наклонных.
Если можно с Дано пожалуйста

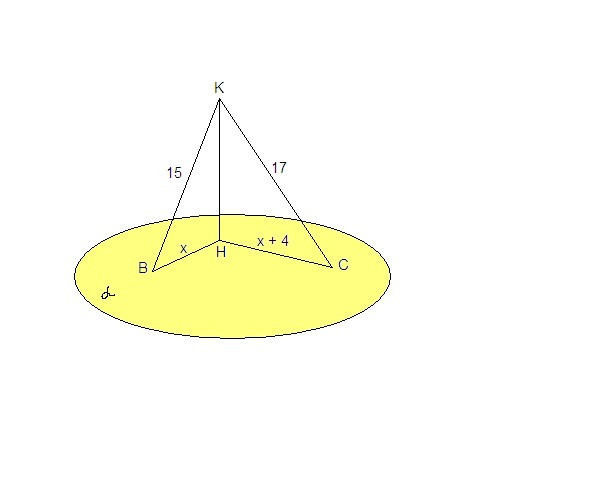
Дано: плоскость α, К∉α,
           КВ = 15 см и КС = 17 см - наклонные
Найти: проекции наклонных на плоскость α.
Решение:
Пусть  КН - перпендикуляр к плоскости α..
Тогда ВН и СН - проекции наклонных на плоскость.
Из двух наклонных, проведенных из одной точки, большую проекцию имеет большая наклонная.
Пусть ВН = х, СН = х + 4

ΔКВН и ΔКСН прямоугольные. По теореме Пифагора выразим из них КН:
КН² = АВ² - ВН² = 225 - х²
КН² = АС² - СН² = 289 - (х + 4)²

225 - х² = 289 - (х + 4)²
225 - x² = 289 - x² - 8x - 16
8x = 48
x = 6

ВН = 6 см
СН = 10 см