Предмет: Геометрия
Автор: Alijon004
Вопрос задан 2 года назад

< >

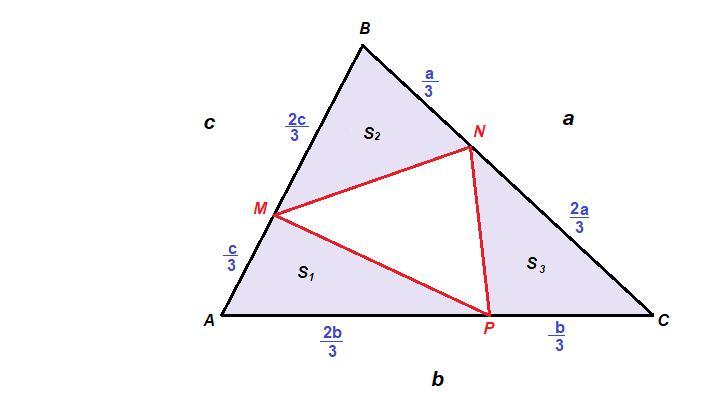
На сторонах треугольника ABC взяты точки M,N,P так,что они делят стороны AB,BC,CA в отношении 1:2, считая с вершины A,B,C. Найдите площадь треугольника MNP, если известно,что площадь треугольника ABC равна S

Ответы

Ответ дал: KuOV

Ответ:

$S_{MNP}=\dfrac{S}{3}$

Объяснение:

Обозначим стороны треугольника:

АВ = с

AC = b

BC = a

Площадь треугольника АВС:

$S_{ABC}=\dfrac{1}{2}ab\cdot \sin C=\dfrac{1}{2}bc\cdot \sin A=\dfrac{1}{2}ac\cdot \sin B=S$

Площади "отсекаемых треугольников":

$S_1=\dfrac{1}{2}\cdot \dfrac{c}{3}\cdot \dfrac{2b}{3}\cdot \sin A=\dfrac{bc}{9}\cdot \sin A$

$S_2=\dfrac{1}{2}\cdot \dfrac{a}{3}\cdot \dfrac{2c}{3}\cdot \sin B=\dfrac{ac}{9}\cdot \sin B$

$S_2=\dfrac{1}{2}\cdot \dfrac{b}{3}\cdot \dfrac{2a}{3}\cdot \sin C=\dfrac{ab}{9}\cdot \sin C$

Найдем, какую часть они составляют от площади треугольника АВС:

$\dfrac{S_1}{S_{ABC}}=\dfrac{bc}{9}\cdot \sin A:\left(\dfrac{1}{2}bc\cdot \sin A\right)=\dfrac{1}{9}\cdot 2=\dfrac{2}{9}$

$S_1=\dfrac{2}{9}S$

Аналогично,

$S_2=\dfrac{2}{9}S$

$S_3=\dfrac{2}{9}S$

Тогда площадь треугольника MNP:

$\boldsymbol{S_{MNP}}=S_{ABC}-S_1-S_2-S_3=S-3\cdot \dfrac{2}{9}S=S-\dfrac{2}{3}S=\boldsymbol{\dfrac{1}{3}S}$

Приложения:

Похожие вопросы

Русский язык

1 год назад

Где предложение а где словосочитание? Свободная тема, Сегодня рисовал маркерами, моё хобби, Всем привет!, Нравиться?, Рисую маркерами

Русский язык

1 год назад

составьте словосочетания с данными глаголами словосочетания укажите форму зависимого от глагола существительного ПЖЖ ОЧЕНЬ НУЖНА СРОЧНАА 10 баллов ПЖЖ ПОМОГИТЕ

Информатика

2 года назад

Помогите решить тест плиз!! срочно! 1.Массив D состоит из действительных чисел от 0.1 до 0.9 с шагом 0.1. Определите формулу для заполнения массива: 1)D[i]:=i*0.1 2)D[i]:=i+0.1 3)D[i]:=i*0.1*0.1

Биология

2 года назад

какие доказательства эволюции животных получены при изучении ископаемых остатков

Химия

7 лет назад

Помогите с химией пожалуйста

Биология

7 лет назад

Помогите с биологией

Математика

9 лет назад

Матиматика планета знаний 2 класс 1 часть стр 46 зад 3

Математика

9 лет назад

Минутная стрелка за 1 час делает круг 31.4 см сколько длина минутной стрелки