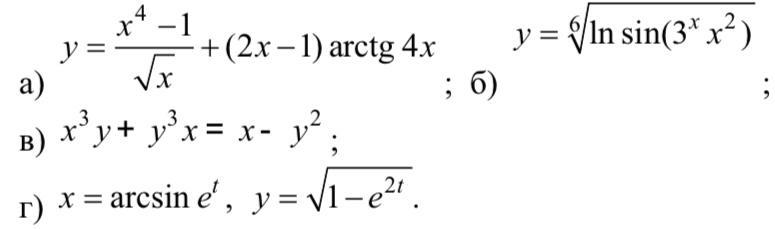Предмет: Математика
Автор: frolliz35
Вопрос задан 2 года назад

< >

Помогите, пожалуйста!
Найти производную dy/dx, если:

Приложения:

Ответы

Ответ дал: Miroslava227

1

Ответ:

а)

$y '= \frac{4 {x}^{3} \times \sqrt{x} - \frac{1}{2 \sqrt{x} }( {x}^{4} - 1) }{x} + 2arctg(4x) + (2x - 1) \times \frac{1}{1 + 16 {x}^{2} } \times 4 = \\ = 4 {x}^{2} \sqrt{x} - \frac{ {x}^{4} - 1}{2x \sqrt{x} } + 2arctg(4x) + \frac{4(2x - 1)}{16 {x}^{2} + 1 }$

б)

$y' = \frac{1}{6} {( ln( \sin( {3}^{x} {x}^{2} ) ) }^{ - \frac{5}{6} } \times \frac{1}{ \sin( {3}^{x} {x}^{2} ) } \cos( {3}^{x} {x}^{2} ) \times ( ln(3) \times {3}^{x} {x}^{2} + 2x \times {3}^{x} ) = \\ = \frac{ctg( {3}^{x} {x}^{2}) }{6 \sqrt[6]{ {ln}^{5} ( \sin( {3}^{x} {x}^{2} )) } } \times {3}^{x} ( ln(3) {x}^{2} + 2x)$

в)

${x}^{3} y + {y}^{3} x = x - {y}^{2}$

$3 {x}^{2} y + y'{x}^{3} + 3 {y}^{2} y'x + {y}^{3} = 1 - 2yy' \\ y' {x}^{3} + 3 {y}^{2} y'x + 2yy' = - 3 {x}^{2} y - {y}^{3} + 1 \\ y'( {x}^{3} + 3x {y}^{2} + 2y) = 1 - {y}^{3} - 3 {x}^{2} y \\ y' = \frac{1 - {y}^{3} - 3 {x}^{2} y}{ {x}^{3} + 3x {y}^{2} + 2y }$

г)

$y'x = \frac{y't}{x't} \\$

$y't = \frac{1}{2} \times \frac{1}{ \sqrt{1 - {e}^{2t} } } \times ( - 2 {e}^{2t} ) = \\ = - \frac{ {e}^{2t} }{ \sqrt{1 - {e}^{2t} } }$

$x't = \frac{1}{ \sqrt{1 - {e}^{2t} } } \times {e}^{t} \\$

$y'x = \frac{ - {e}^{2t} }{ \sqrt{1 - {e}^{2t} } } \times \frac{ \sqrt{1 - {e}^{2t} } }{ {e}^{t} } = \\ = - {e}^{t}$

Аноним: Здравствуйте! Вы не могли бы вы мне помочь с алгеброй пожалуйста)

Похожие вопросы

Русский язык

1 год назад

Летом Марта и Антон приехали к дяде в деревню. Утром дядя Густав отвёз их на машине на хутор к бабушке. Домик бабушки стоял на берегу озера Разнас. По озеру плавали лебеди. Марта и Антон кормили

Русский язык

1 год назад

что означает словосочетание город мира

Английский язык

2 года назад

Напишите как читается (по русски, не перевод), только прошу точней. The problem of learning foreign languages is very important today. They became important especially at the present time. Foreign

Русский язык

2 года назад

сделайте вариант уровень 3 вариант 1

Информатика

7 лет назад

1) Изобразите в декартовой прямоугольной системе координат область, в которой истинны следующие логические выражения: (x >= - 6) и (x <= 6) и (y >= -8) и (y <= 8) 2)Исполнителю

Математика

7 лет назад

знайди пяту частину від 40, тритину від року , сьому частину від тижня, кількість днів у 9 тижнях

Химия

9 лет назад

какой объем занимает сернистый газ (SO2)количеством 0,3моль (н.у)? 1)0,672л.2)672л.3)6,72л.4)67,2л

Биология

9 лет назад

Перша допомога при травмах опорно рухової системи