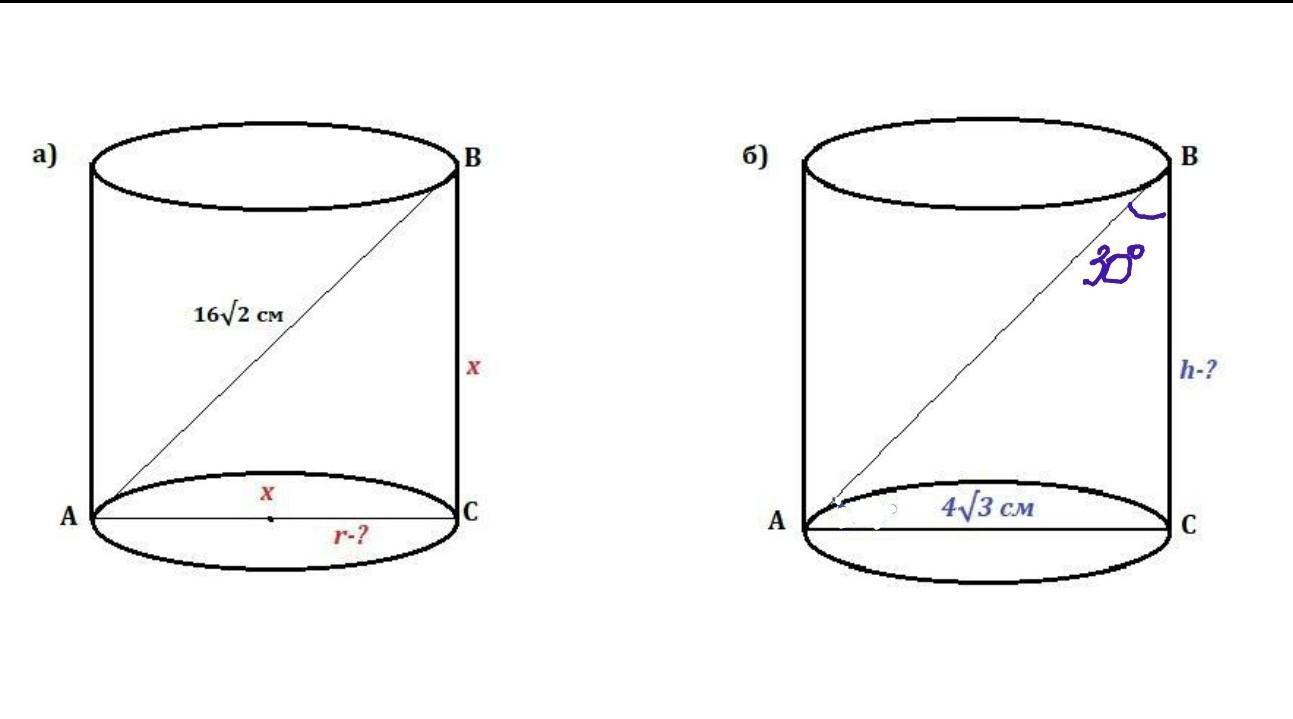
а) Диагональ осевого сечения равностороннего цилиндра равна 16 корень 2 см. Чему равен радиус основания цилиндра? б)Найдите высоту цилиндра, если диагональ его осевого сечения составляет с образующей цилиндра угол 30 градусов, а диаметр его основания равен 4 корен 3 см.
Ответы
Ответ:
а) 8 см
б) 12 см
Объяснение:
а) РАВНОСТОРОННИЙ ЦИЛИНДР — это цилиндр, высота которого равна диаметру его основания.
Осевое сечение цилиндра является прямоугольником.
Высота ВС равна диаметру АС.
⇒Осевое сечение равностороннего цилиндра является квадратом.
Квадрат - это прямоугольник у которого все стороны равны.
АВ - диагональ квадрата.
Так как диагональ квадрата равна стороне квадрата, умноженной на корень из двух, то:
АВ = √2*АС, 16√2=√2*АС, АС = 16 см
Радиус основания цилиндра равен половине диаметра:
Радиус основания равен 8 см
б) Осевое сечение цилиндра является прямоугольником.
ВС - образующая цилиндра. ∠АВС = 30°.
Так как АС⊥ВС, рассмотрим прямоугольный треугольник АВС(∠С=90°).
Котангенс угла – это отношение прилежащего катета к противолежащему.
Высота цилиндра равна 12 см.