ТЕРМІНОВО! 50 б.
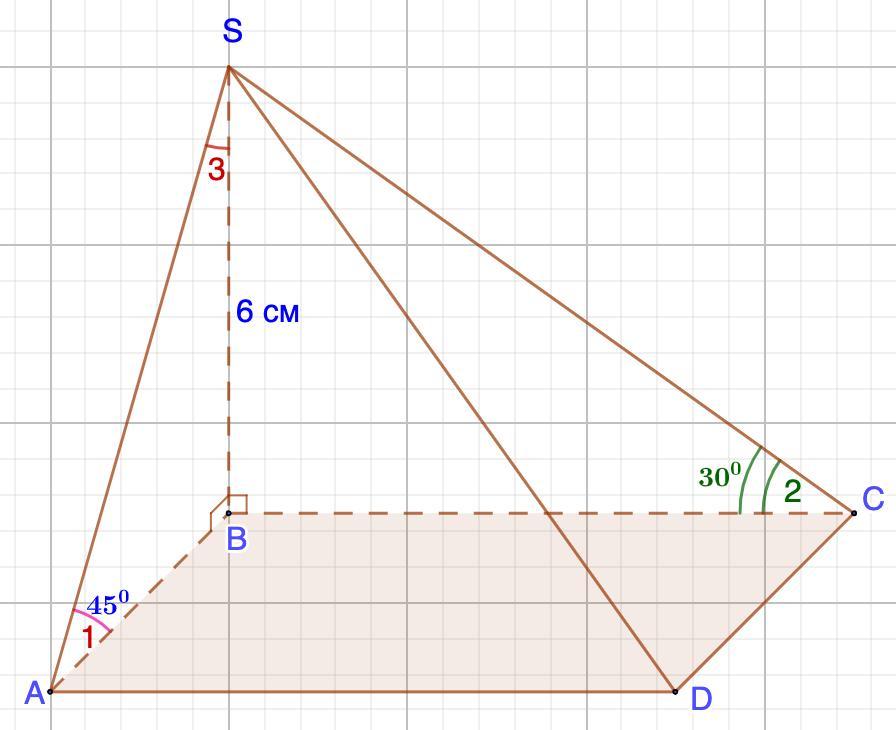
Основою піраміди є прямокутник . Висота піраміди проходить через одну з його вершин . Бічні грані , що не містять висотк , нахилені до площини основи під кутами 30° і 45°. Знайдіть об'єм піраміди , якщо її висота дорівнює 6 см

Ответ:

72√3 см³

Объяснение:

Дано: SABCD - пирамида;

ABCD - прямоугольник;

SB⊥ABCD;

∠1=45°; ∠2=30°; SB=6 см.

Найти: .

Решение:

1. Рассмотрим ΔSAB - прямоугольный.

∠3=90°-∠1 (сумма острых углов прямоугольного Δ-ка)

∠3=90°-45°=45°

⇒ ΔSAB - равнобедренный.

⇒ AB=BS=6 см.

2. Рассмотрим ΔSBС - прямоугольный.

∠2=30° ⇒ SC=2SB =12 (см) (катет, лежащий против угла 30°)

По теореме Пифагора:

(см)

3. Найдем площадь основания и объем пирамиды:

(см²)

(см³)