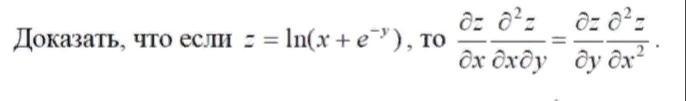Предмет: Математика
Автор: khabibulina200
Вопрос задан 2 года назад

< >

Помогите решить. Доказать, что если z=ln9x+e^-y), то

Приложения:

Ответы

Ответ дал: Miroslava227

0

Ответ:

$\frac{dz}{dx} = \frac{1}{x + {e}^{ - y} } \times 1 \\$

$\frac{ {d}^{2} x}{dxdy} = - {(x + {e}^{ - y}) }^{ - 2} \times ( - {e}^{ - y} ) = \\ = \frac{ {e}^{ - y} }{ {(x + {e}^{ - y} )}^{2} }$

$\frac{dz}{dy} = - \frac{ {e}^{ - y} }{x + {e}^{ - y} } \\$

$\frac{ {d}^{2}z }{ {dx}^{2} } = - {(x + {e}^{ - y} )}^{ - 2} \times 1 = \\ = - \frac{1}{ {(x + {e}^{ - y}) }^{2} }$

подставляем в равенство:

$\frac{1}{x + {e}^{y} } \times \frac{ {e}^{ - y} }{(x + {e}^{ - y} ) ^{2} } = - \frac{ {e}^{ - y} }{x + {e}^{ - y} } \times ( - \frac{1}{ {(x + {e}^{ - y} )}^{2} } ) \\ \frac{ {e}^{ - y} }{ {(x + {e}^{ - y}) }^{ 3} } = \frac{ {e}^{ - y} }{ {(x + {e}^{ - y}) }^{3} }$

tiharo3463: Здравствуйте, вы можете помочь с задачей? Спасибо) https://znanija.com/task/41872788

Похожие вопросы

Английский язык

1 год назад

Помогите плизз. ;з Или скиньте Г.Д.З. на это

Беларуская мова

1 год назад

Ьхелп,срочно надопомогите.очень нужно,помогите!!!

Физика

2 года назад

Помогите решить эту легкую задачу... Очень нужно

Математика

2 года назад

Даю 30 баллов Решите уравнения Б)18/25*6/35=t*27-175 В)t*8/13=28/91*6/7

Биология

7 лет назад

Помогите, срочнооо пожалуйста

Математика

7 лет назад

помогите пожалуйста а + в = 60 а - в = 40 а/в - ?

Литература

9 лет назад

які є історизми укрлітература

Математика

9 лет назад

Упростите отношения №1 (все номера сделать с решениями и пояснениями прошу) а) 27:45 (дробь) б) 18/63 (дробь) в) 28кг/49кг (дробь) г) 12м/3600см (дробь) №2 Разделите число 140 в отношении 3:4.