• Предмет: Математика
  • Автор: ilnuribragimov812199
  • Вопрос задан 2 года назад
< >

Помогите решить задачу, необходим рисунок

Приложения:

Ответы

Ответ дал: pushpull
1

Ответ:

Пошаговое объяснение:

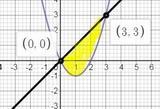
делаем чертеж и из него сразу всё видно

у₁ = х (график лежит "выше")

у₂ = х² -2х

пределы интегрирования по х от 0 до 3

считаем площадь

S=\int\limits^3_0 {(x-x^2+2x)} \, dx= \int\limits^3_0 {(-x^2+3x)} \, dx =-\int\limits^3_0 {(x^2)} \, dx +3\int\limits^3_0 {(x)} \, dx =

=-\frac{x^3}{3} I_0^3+\frac{3x^2}{2} I_0^3=-9+\frac{27}{2} =\frac{9}{2}

Приложения:
Похожие вопросы
Другие предметы
1 год назад
как раньше называли охранников ​
Английский язык
1 год назад
Е. заполните пропуски используя слова данные в рамке. F. соедините две части предложения.
Математика
2 года назад
Самокат и собачонка Весят, как одна девчонка .Шустрый пес без самоката Весит точно ,как котята,Их в лукошке ровно пять,Можешь ты теперь узнать Сколько весит та девчонка В пересчете на котенка.Но при
Математика
2 года назад
Что больше? 2\5 т или 3\4 т? 5\8 км или 3\5 км? 4\5 мин или 4\6 мин?
Информатика
7 лет назад
Составьте блок схему c++
Математика
7 лет назад
Определи коэффициенты a, b и c линейного уравнения с двумя переменными: 2x+y−3=0. Ответ: a= ? ; b= ? ; c= ? .
Химия
9 лет назад
Дано 32 грамма оксида железа 3, сколько моли это состовляет
Математика
9 лет назад
Д-множество двузначных чисел в которых разряде единиц на 3 больше разряда десятков Сколько элементов в данном множестве?