Дан∠A = 30° , ∠ABC=60°, BD перпендикулярна к плоскости ABC. Доказать,что CD перпендикулярно AC. Нужно применить теорему о трёх перпендикулярах и написать,где именно применить.

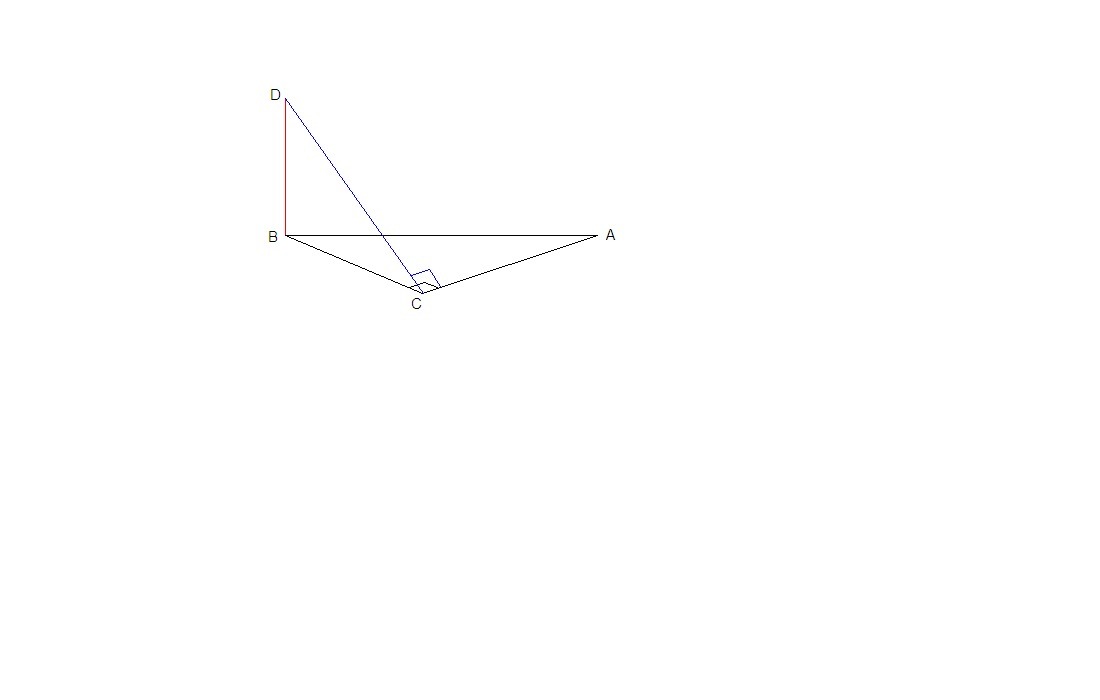
В треугольнике АВС ∠А = 30°, ∠В = 60°, значит ∠С = 90°.
DC - наклонная к плоскости АВС,
DB - перпендикуляр к АВС, значит
ВС - проекция наклонной DC на плоскость АВС.

ВС⊥АС, значит и DC⊥AC по теореме о трех перпендикулярах (если прямая, лежащая в плоскости, перпендикулярна проекции наклонной на эту плоскость, то она перпендикулярна и самой наклонной)