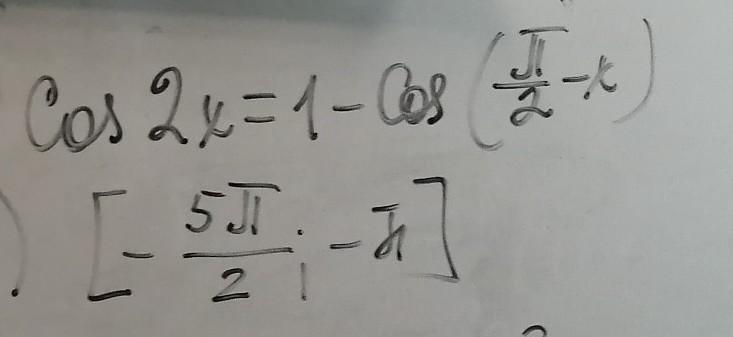Предмет: Математика
Автор: NAZARIONYOUTUBE
Вопрос задан 2 года назад

< >

решите тригонометрию, пожалуйста

Приложения:

Ответы

Ответ дал: Miroslava227

0

Ответ:

$\cos(2x) = 1 - \cos( \frac{\pi}{2} - x) \\ \cos(2x) = 1 - \sin(x) \\ 1 - 2 { \sin }^{2} (x) - 1 + \sin(x) = 0 \\ - 2 { \sin}^{2} (x) + \sin(x) = 0 \\ - \sin(x) ( 2 \sin(x) - 1) = 0 \\ \\ \sin(x) = 0 \\ x1 = \pi \: n \\ \\ 2 \sin(x) - 1 = 0 \\ \sin(x) = \frac{1}{2} \\ x2 = \frac{\pi}{6} + 2 \pi \: n \\ x3 = \frac{5\pi}{6} + 2 \pi \: n$

n принадлежит Z.

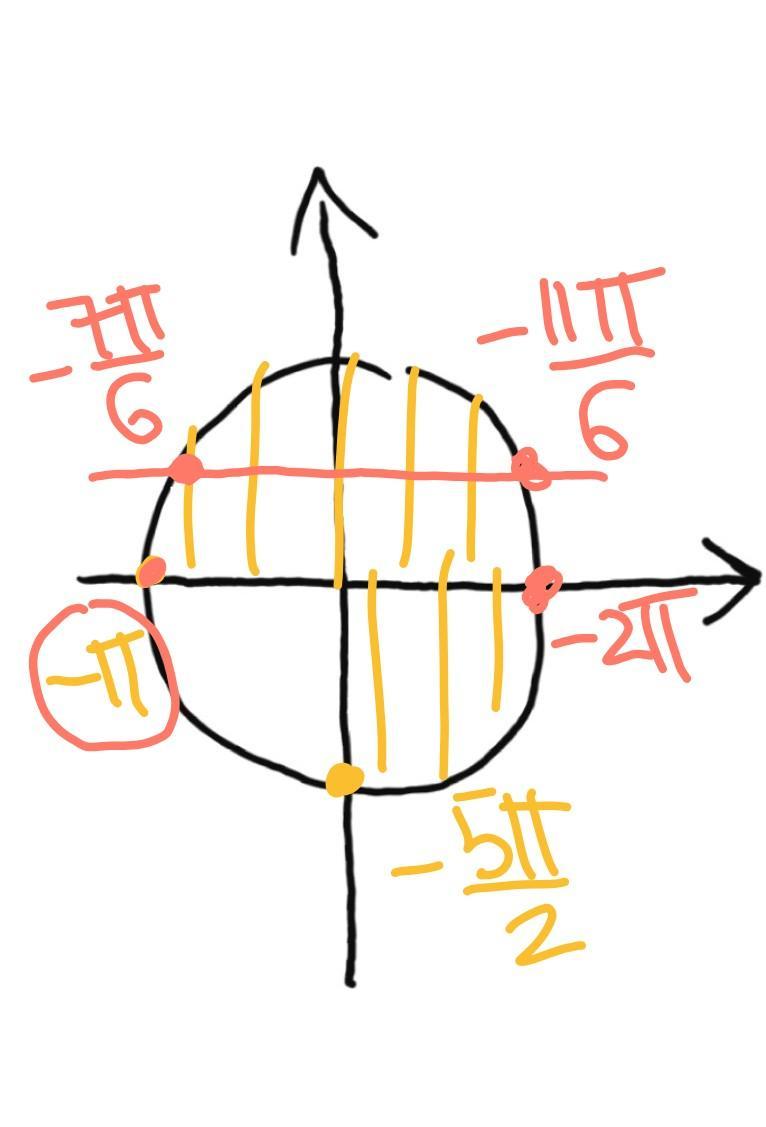
на промежутке:

[-5П/2;-П]

-2П; -11П/6; -7П/6; -П

Ответ:

$a)x1 = \pi \: n \\ x2 = \frac{\pi}{6} + 2\pi \: n \\ x2 = \frac{5\pi}{6} + 2\pi \: n \\ \\ b) - 2\pi ;- \frac{11\pi}{6} ; - \frac{7\pi}{6}; - \pi$

Приложения:

Похожие вопросы

Русский язык

1 год назад

Написать рекламный текст для посетителей выставки тюльпанов с использованием в тексте предложений с тире между подлежащим и сказуемым? 6-7 предложений.

Қазақ тiлi

1 год назад

помогите пожалуйста ответить на вопросы по казаскому языку

Русский язык

2 года назад

Сочинение на тему "Моя малая родина". Люди, не подведите, я в вас верю! Сочинение нужно как можно быстрее, и не скачанное из инета!

Русский язык

2 года назад

сливки духи макароны. что общего у этих слов

Математика

7 лет назад

Я совсем не понимаю задачи на движение. Можете пожалуйста объяснить задачу номер 4(Во вложении) СРОЧНО! 20 БАЛЛОВ)

Литература

7 лет назад

Напишите сочинение по плану по поэме Твардовского "Василий Тёркин" срочно 300-400 слов

География

9 лет назад

Используя свои знания по истории, объясните, почему стран с монархической формой правления больше всего в зарубежной Европе и зарубежной Азии, а в Северной Америке их вообще нет.. помогите

Математика

9 лет назад

Решите пожалуйста 13,6*x-3,64=1,8