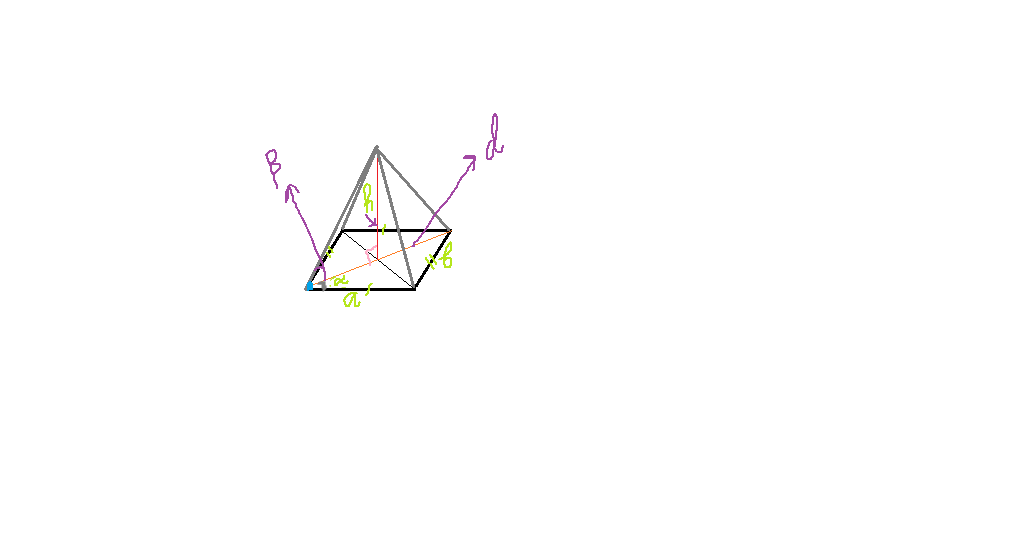
Основанием пирамиды является прямоугольник со стороной А. Угол между этой стороной и диагональю прямоугольника равен АЛЬФА. Найдите обьём пирамиды, если каждое её ребро наклонено к плоскости основания под углом БЕТА.
Ответы
Ответ дал:
0
1) d=a/cosα
b²=d²-a²=a²/cos²α - a²=a²(1-cos²α)/cos²α=a²*tgα
b=a*tgα
2) tgβ=2h/d h=d*tgβ/2=a*tgβ/2cosα
S=ab=a²*tgα
V=S*h/3=a³*tgα*tgβ/6cosα
b²=d²-a²=a²/cos²α - a²=a²(1-cos²α)/cos²α=a²*tgα
b=a*tgα
2) tgβ=2h/d h=d*tgβ/2=a*tgβ/2cosα
S=ab=a²*tgα
V=S*h/3=a³*tgα*tgβ/6cosα
Приложения:
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад