ОЧЕНЬ СРОЧНО!!! ПОЖАЛУЙСТА
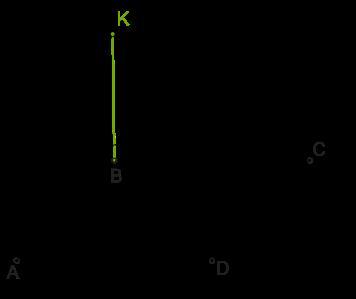
От вершины K к плоскости квадрата ABCD проведена прямая KB так, что ∡KBA=90° и ∡KBC=90°.
Рассчитай расстояние от K к вершинам квадрата, если сторона квадрата равна 3 см, а KB = 19 см.

Ответы введи округлёнными до одной десятой:

KA =
см;

KC =
см;

KD =
см.

Приложения:

Ответы

Ответ дал: 25hjoerf10

Ответ: KA = 19,2 см; KC = 19,2 см; KD = 19,5 см.

Объяснение:

Найдем диагональ квадрата BD:

$BD=\sqrt{3^{2} +3^{2} } =\sqrt{18} =3\sqrt{2}$

Расстояние от К до D:

$KD=\sqrt{KB^{2}+BD^{2} } =\sqrt{19^{2}+(3\sqrt{2})^{2} } =\sqrt{361+18} =\sqrt{379} \approx 19,4679223339$

KD = 19,5 см

Расстояние от K до A:

$KA=\sqrt{AB^{2}+KB^{2} } =\sqrt{3^{2}+19^{2} } =\sqrt{370} \approx 19,2353840617$

KA = 19,2 см

Расстояние от K до С:

KC = KA = 19,2 см

Похожие вопросы

Английский язык

1 год назад

Русский язык

1 год назад

Математика

2 года назад

Алгебра

2 года назад

Геометрия

7 лет назад

Математика

7 лет назад

Математика

9 лет назад

Математика

9 лет назад