Предмет: Алгебра
Автор: AMSS
Вопрос задан 10 лет назад

< >

Алгебра, 10 класс. Буду очень благодарна, если поможете)
cos^6x+sin^6x=7/16
(на фото 23.24 а))

Приложения:

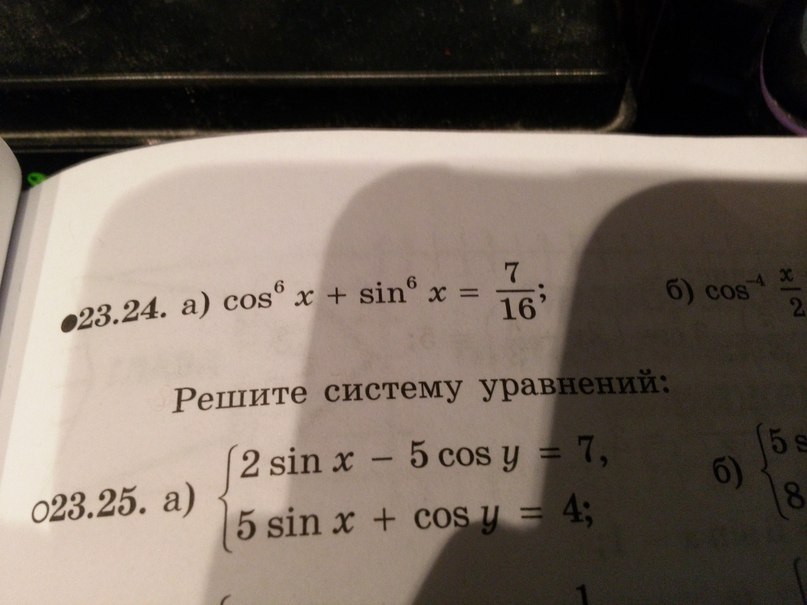
Ответы

Ответ дал: Матов

0

$cos^6x+sin^6x = (cos^2x+sin^2x)(cos^4x-cos^2x*sin^2x+sin^4x)\ (cos^2x+sin^2x)(cos^4x-cos^2x*sin^2x+sin^4x)=frac{7}{16}\ cos^4x-cos^2x*sin^2x+sin^4x=frac{7}{16}\ 3cos^4x-3cos^2x+1=frac{7}{16}\ 3cos^4x-3cos^2x-frac{9}{16}=0\ cos^2x=t\ 3t^2-3t+frac{9}{16} = 0 \ D=9-4*3*frac{9}{16} = (1.5)^2\ t=frac{3+1.5}{6}= frac{3}{4}\ t=frac{3-1.5}{6}= frac{1}{4}\ cosx=frac{sqrt{3}}{2}\ cosx=frac{1}{2} \ x= - frac{pi}{6}+frac{pi*k}{2};\ x= - frac{pi}{6}+frac{pi*k}{2}$

Ответ дал: AMSS

0

в той же четвертой строчке, откуда тройка?

Ответ дал: Матов

0

я же говорю после преобразований все вышло

Похожие вопросы

Английский язык

2 года назад

30 баллов. Помогите составить 10-15 предложений на английском про моего друга и его семью ( семейные традиции и все в этом роде, тут в основном рассказываться про его семью, а не про него самого)

Русский язык

2 года назад

Объясните смысл пословицы ,,никакой лимон сладким не сделаешь''

Химия

7 лет назад

Ребят, срочно! Помогите пожалуйста с химией составьте уравнения реакций бут-1-ен с водородом и бромом взятыми в избытке. назовите продукты реакции (складіть рівняння реакцій бут-1-ену з воднем і

Химия

7 лет назад

классицурйте вещества и назовите Fe, K²CO³, HCI, AgNO³

Алгебра

10 лет назад

Помогите решить, всё забыл))) Спасибо!

Математика

10 лет назад

как решить этот пример: 36*4-(15+52)*3+48/24*9

Геометрия

10 лет назад

На поверхности шара даны три точки, расстояние между которыми равны 12, 16, 20 см. Расстояние от центра шара до плоскости, проведённой через эти точки, 24 см. Вычислите длину окружности большого

Литература

10 лет назад

Напишите письмо своему сверстнику который хочет изучать английский язык самостоятельно. Можете кратко , ОЦЕНЮ И ПОБЛАГОДАРЮ ЛЮБУЮ ПОМОЩБ