AB=BC FD=FC доказать что AB паралельно DF​

Ответ:

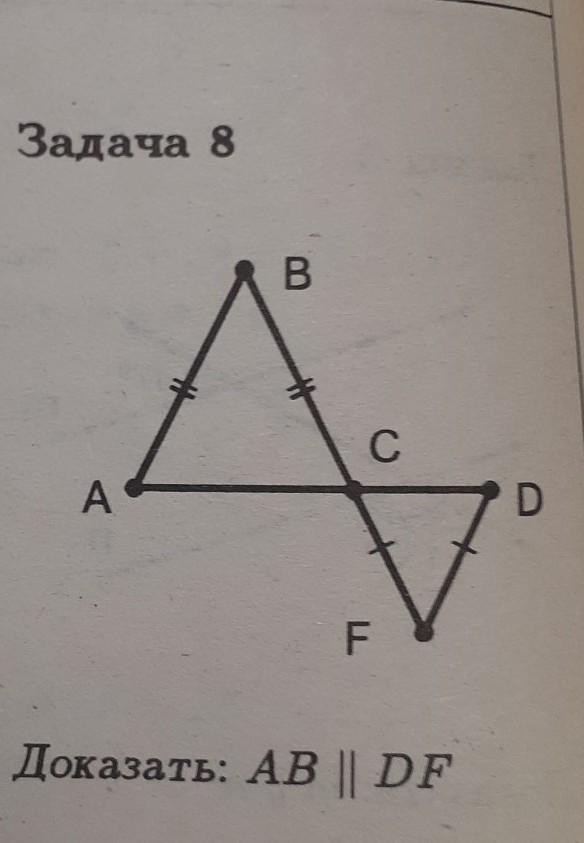
рассмотрим треугольники ABC, CDF у них:

АВ=ВС,СФ=ДФ,

Решение:

Рассмотрим тр. АВС. Т. к. АВ = ВС, тоо он равнобедренный. Значит, у него углы при основании (ВАС и ВСА) будут равны. Углы ВСА и FCD - вертикальные, значит угол ВСА = углу FCD.

Рассмотрим тр. FCD. Он тоже будет равнобедренным, ведь FC = FD, значит угол FCD = FDC.

А то есть, угол BAC=BCA=FCD=FDC. Из этого равенства получаем, что угол ВАС = FDC , а они же накрест лежащие при прямых АВ и FD и секущей ВF. А если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. А значит, что AB || DF.