Пожалуйста помогите с этим неравенством
Приложения:
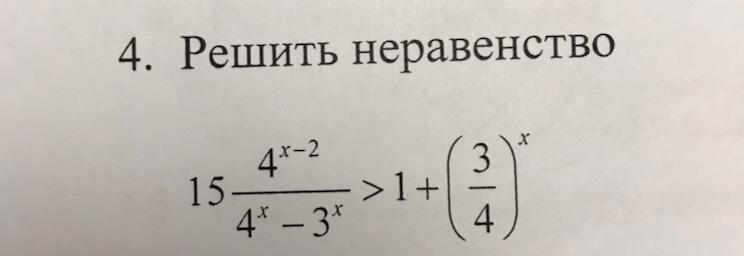
LFP:
замена: t=(3/4)^x; t>0... а дробь в левой части равенства сократить на 4^х (которое не равно нулю) и получим: 1 / (16(1-t)) > 1+t обычное (уже не показательное) дробное неравенство, которое решается методом интервалов...
Ответы
Ответ дал:
0
Ответ:
1>x>log(0,75)(0,25)
Пошаговое объяснение:
Поделим числитель и знаменатель дроби на 4^x. y=(3/4)^x
(15/16)*(1/(1-y)>1+y
ясно, что 1-y>0 1>у
Умножим все на 1-y
(15/16)>1-y^2
y^2>1/16
значит либо у больше 1/4 либо у меньше -1/4
Однако у больше 0. Поэтому гдитс лишь 1>y>1/4
(3/4)^x<1 значит х >1
(3/4)^x>(1/4)
справа функция монотонно убывающая.
Значит 1>x>log(0,75)(0,25)
Похожие вопросы
1 год назад
1 год назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад