Точка K лежит внутри квадрата ABCD со стороной α, ∠KAD =∠KDA = 15°. Доказать, что BK = KC = α (привести геометрическое доказательство без использования теоремы косинусов и тригонометрических формул). 

т.к. углы равны КAD = KDA => AKD -- равнобедренный
треугольники AKВ и DKC равны по двум сторонам и углу между ними
(BA=CD --- т.к. квадрат, АК=KD --- т.к. AKD равнобедренный,
угол ВАК=CDK = 90-15 = 75 градусов)))
=> BK = KC 
понятно, что нужно было поискать треугольник с углами 30 и 60 градусов...
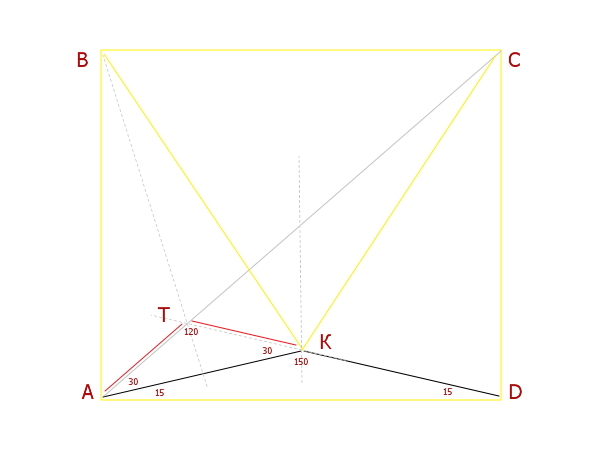
я продолжила сторону KD до пересечения с диагональю АС в точке Т --- получился треугольник АТD с углами 15, 45, 120...
провела ВТ...
угол ТАК=30=ТКА следовательно BT _|_ AK
и в треугольнике АТК эта прямая --- медиана,
значит и для АВК эта прямая ВТ и медиана и высота,
т.е. АВК --- равнобедренный и
АВ=ВК=а

спасибо за задачу... искать решение было здорово...

обратитесь к Hrisula , она дает разрешение на повторную корректировку решения