Предмет: Алгебра
Автор: russianen
Вопрос задан 10 лет назад

При каких значениях параметра a уравнение x^2-9/x-a=0,имеет единственное решение?

Ответы

Ответ дал: Vladislav006

Уравнение $x^2 - frac{9}{x} - a = 0$

ОДЗ: $x neq 0$ - в этой точке функция не определена, т.е. имеет разрыв.

Проведем исследование с помощью производной
$y' = (x^2 - frac{9}{x} - a)' = 2x + frac{9}{x^2}$

Найдем критические точки
$2x + frac{9}{x^2} = 0 \ \ 2x^3 + 9 = 0 \ \ x = - sqrt[3]{ frac{9}{2} } approx -1,65$
Исследуем знак производной слева и справа от критических точек (-1,65) и (0)
$y'(-3) = 2 * (-3) + frac{9}{(-3)^2} = -5 textless 0 \ \ y'(-1) = 2 * (-1) + frac{9}{(-1)^2} = 7 textgreater 0$

Производная меняет знак с "-" на "+" следовательно, в этой точке $x = - sqrt[3]{ frac{9}{2} }$ функция достигает минимума.

$y'(1) = 2 * 1 + frac{9}{1^2} = 11 textgreater 0$
На интервале $(0; + infty )$ функция возрастает, следовательно на этом интервале всегда будет единственное решение уравнения.

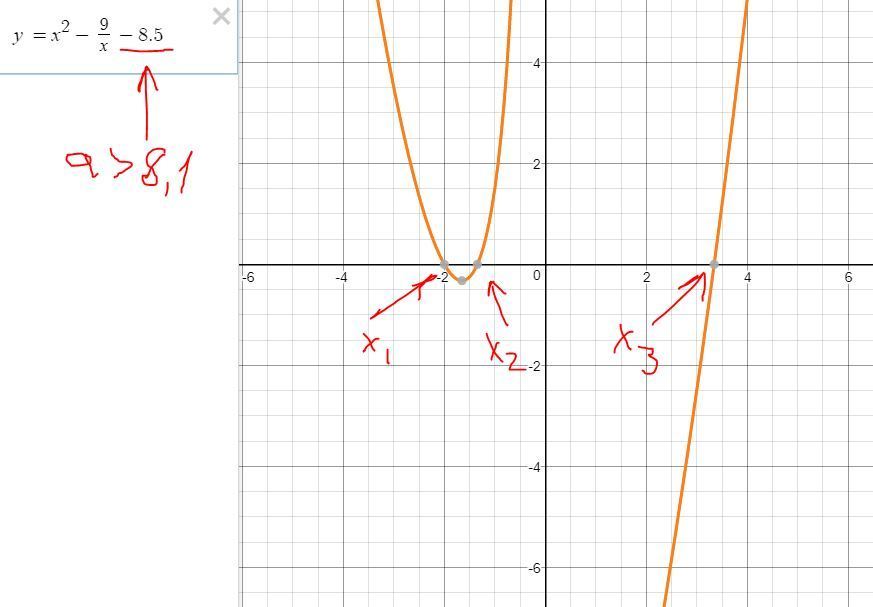
Следовательно необходимо подобрать такой параметр "а", при котором на интервале $(- infty ; 0)$ уравнение не имело бы решения. Иначе уравнение будет иметь более одного решения.

Определим при каком значении параметра "а" уравнение будет иметь касание с осью ОХ.
Для этого подставим в уравнение значение $x = - sqrt[3]{ frac{9}{2} }$

$(- sqrt[3]{ frac{9}{2}})^2 - frac{9}{- sqrt[3]{ frac{9}{2}}} - a = 0$

$(- sqrt[3]{ frac{9}{2}})^2*sqrt[3]{ frac{9}{2}} + 9 - a* sqrt[3]{ frac{9}{2}} = 0$

$frac{9}{2} + 9 = a* sqrt[3]{ frac{9}{2}}$

$a = frac{13,5}{ sqrt[3]{4,5} } = 3 sqrt[3]{20,25} approx 8,177$

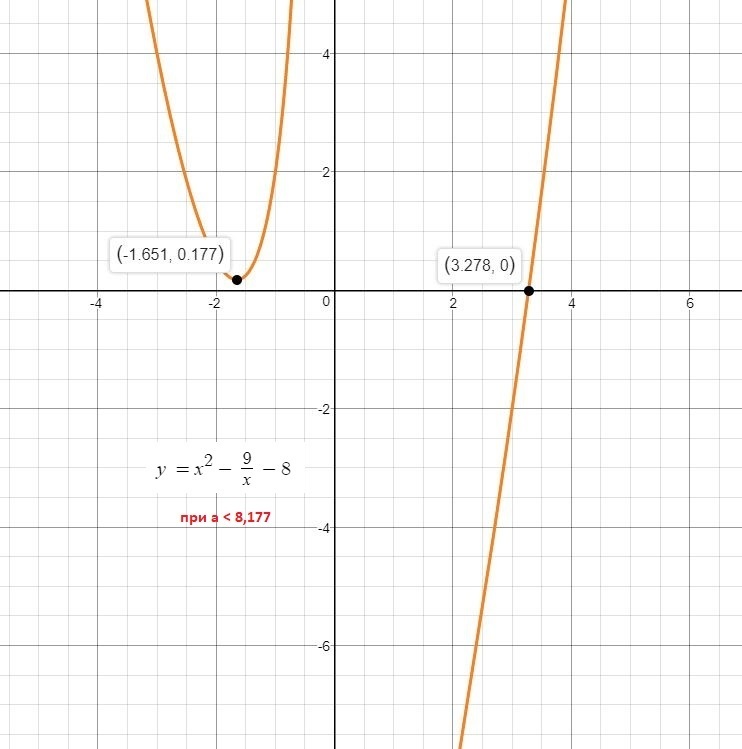
Таким образом, если параметр будет $a textless frac{13,5}{ sqrt[3]{4,5} } approx 8,177$ , то уравнение будет иметь единственное решение.

Это можно также проверить графически, если при а=8 < 8,177 построить график функции $y = x^2 - frac{9}{x} - 8$ . Смотри рисунок ниже.

Ответ: при параметре
$a textless 3 sqrt[3]{20,25} approx 8,177$
уравнение имеет единственное решение.

Проверка: пусть а =0
$x^2-9/x-0=0$
$x^2-9/x=0$
$x^3-9=0 \ x^3=9$
$x= sqrt[3]{9}$ - единственный корень.

!!! Если нужно получить зависимость "Х" (корня) от параметра "а" , то можно воспользоваться формулой Кардано, для неполного кубического уравнения.

Вывод писать не буду, но ответ напишу
$x = sqrt[3]{ frac{9}{2} + sqrt{( frac{-a}{3} )^3+(frac{9}{2})^2}} + sqrt[3]{ frac{9}{2} - sqrt{( frac{-a}{3} )^3+(frac{9}{2})^2}}$

Например, пусть а = 0, тогда
$x = sqrt[3]{ frac{9}{2} + sqrt{( frac{0}{3} )^3+(frac{9}{2})^2}} + sqrt[3]{ frac{9}{2} - sqrt{( frac{0}{3} )^3+(frac{9}{2})^2}} = \ \ = sqrt[3]{ frac{9}{2} + sqrt{(frac{9}{2})^2}} + sqrt[3]{ frac{9}{2} - sqrt{(frac{9}{2})^2}} = \ \ = sqrt[3]{ frac{9}{2} + frac{9}{2}} + 0 = sqrt[3]{9}$

Приложения: