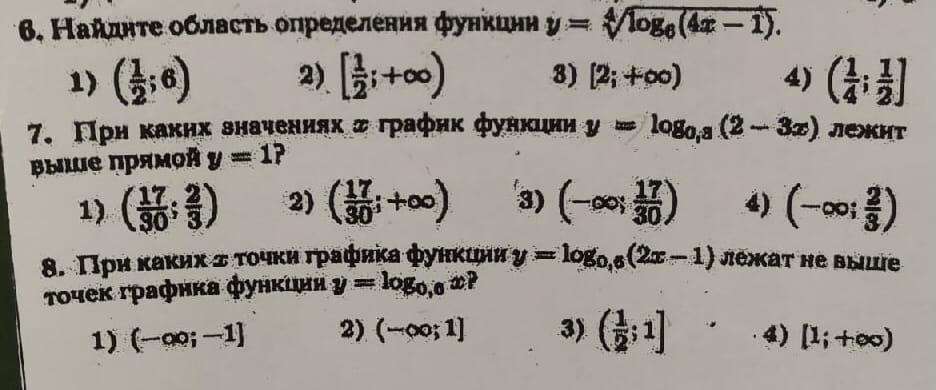Решить все пожалуйста и понятное объяснение

Ответ:

Объяснение:

6.  данная функция является сложной.   корень четной степени - это значит, что значение  под корнем должно быть неотрицательным. т.е.

   решаем данное неравенство.  

далее,  функция логарифмическая,  следовательно величина под знаком логарифма должна быть больше нуля.  

рассматриваем оба неравенства и находим область пересечения интервалов

   x∈ [  +∞   [

7.        значение под знаком логарифма должно быть больше нуля.  2-3х>0   2>3x   x<2/3

рассмотрим условие при котором    у>1

находим область пересечения обоих условий,

   x∈ ] -∞; 7/15 [

8.     область определения функции.    

 2х-1>0      x>1/2

вводим дополнительное условие

    x∈ ] 1;  +∞ [