укажите наибольшее значение, которое может принимать выражение 3x-5y

Приложения:

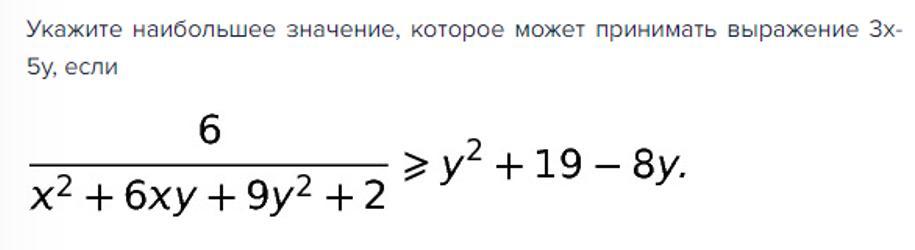
Alexandr130398: -56

Ответы

Ответ дал: ismars

Ответ:

Пошаговое объяснение:

$\frac{6}{x^2+6xy+9y^2+2}\geq y^2-8y+19$

$\frac{6}{(x+3y)^2+2}\geq (y-4)^2+3$

$((y-4)^2+3)((x+3y)^2+2)\leq 6$

Первый множитель не меньше 3, второй не меньше 2. Неравенство выполняется только тогда, когда выполняется следующая система:

$\left \{ {{y-4=0} \atop {x+3y=0}} \right.$

Отсюда y = 4, x = -12. Наибольшее значение выражения 3x-5y равно -56.

olkobzeva11: можно узнать ваши контакты в телеграм/инст? нужна помощь с подобным на экзамене(не за просто так, конечно же)

ismars: Буду рад помочь! Мой инстаграм: ismars_yar

Похожие вопросы

Қазақ тiлi

1 год назад

Английский язык

1 год назад

История

2 года назад

Математика

2 года назад

Литература

7 лет назад

Обществознание

7 лет назад

Математика

9 лет назад

Математика

9 лет назад