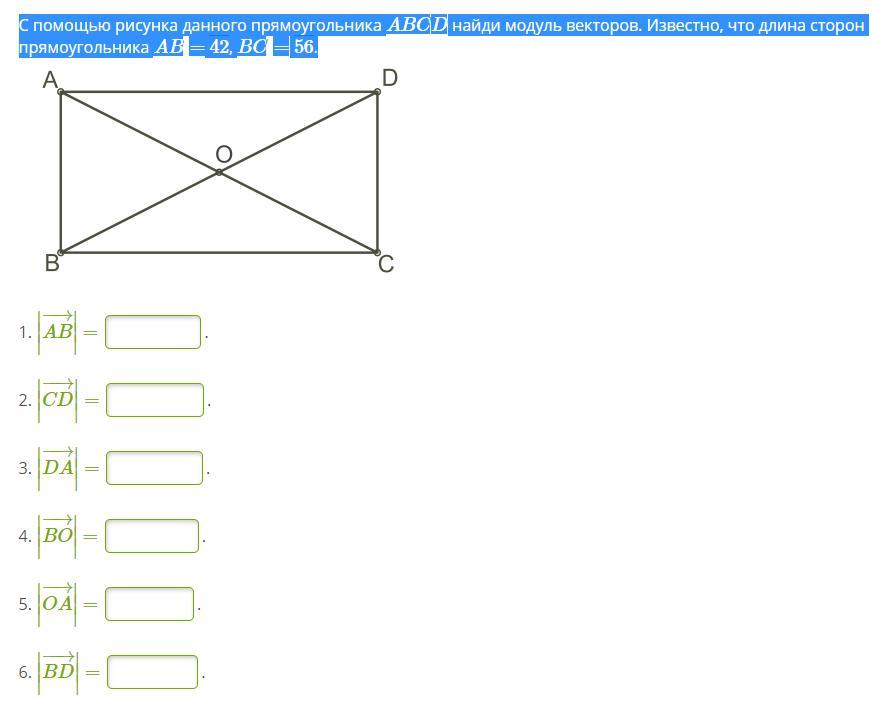
ребят срочно С помощью рисунка данного прямоугольника ABCD найди модуль векторов. Известно, что длина сторон прямоугольника AB= 42, BC= 56.

Ответ:

Модули векторов:

1.

2.

3.

4.

5.

6.

Объяснение:

• Модуль (длина) вектора равна длине соответствующего отрезка.

Противоположные стороны прямоугольника равны.

CD = AB = 42

AD = BC = 56

Из прямоугольного треугольника АВС по теореме Пифагора:

Диагонали прямоугольника равны и точкой пересечения делятся пополам.

BD = AC = 70

AO = BO = CO = DO = 0,5 · AC = 35

Итак, найдены длины всех отрезков. Тогда длины векторов:

1.

2.

3.

4.

5.

6.