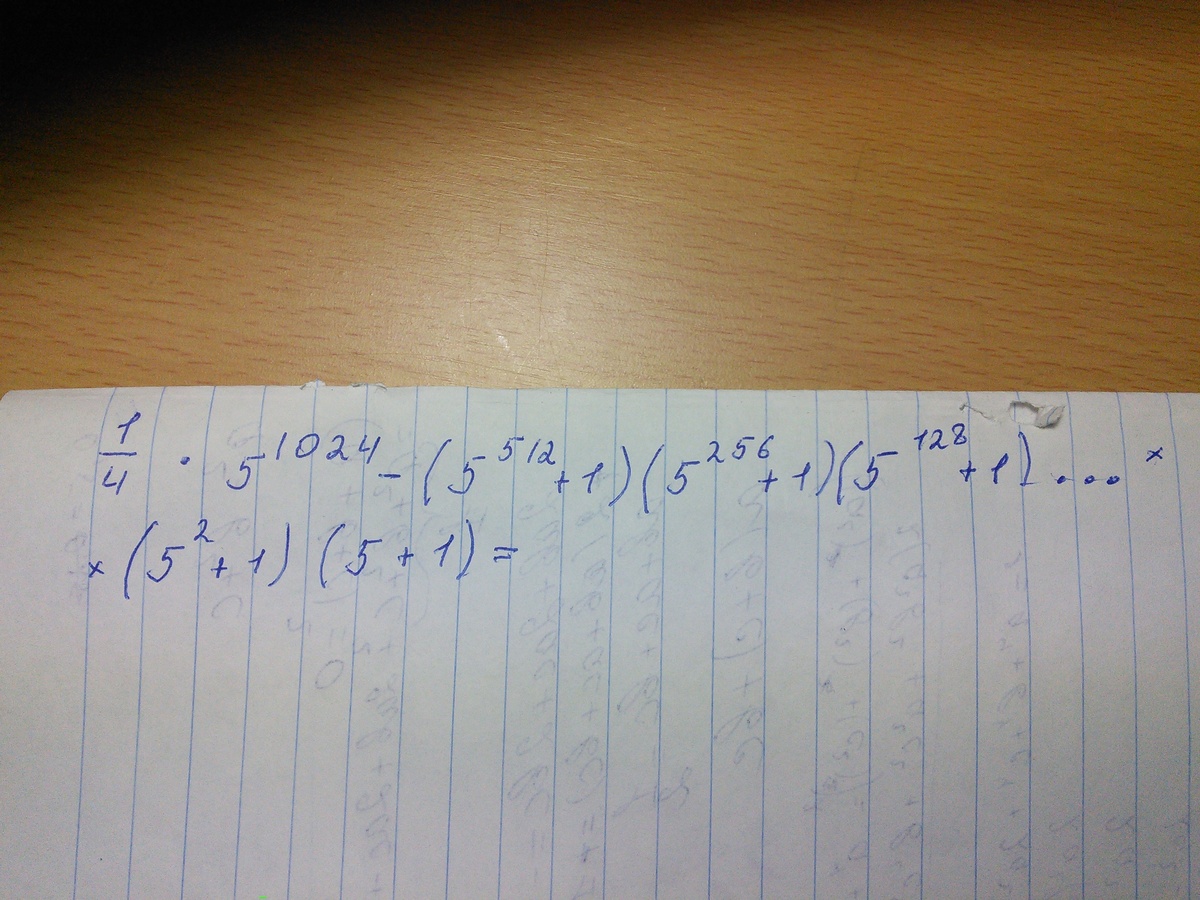Предмет: Алгебра
Автор: sergkru
Вопрос задан 10 лет назад

< >

помогите решить,
задание на фото

Приложения:

Ответы

Ответ дал: Матов

0

$frac{1}{4}*5^{1024}-(5^{512}+1)(5^{256}+1)(5^{128}+1)....(5^4+1)(5^2+1)(5+1)$
если открыть скобки очевидно будет сумма геометрической прогрессий то есть

$frac{1}{4}*5^{1024}-(5^{1023}+5^{1022}+.....1)$
найдем сумму это прогрессий по формуле
$S=frac{b_{1}(q^n-1)}{q-1}$
видно что $q=5$ , вычислим $n$
$b_{1}=1\ q=5\ 5^{1023}=5^{n-1}\ n=1024\\ S=frac{5^{1024}-1}{4}\ \ frac{5^{1024}}{4}-frac{5^{1024}-1}{4}=frac{1}{4}$

Ответ $frac{1}{4}$

Похожие вопросы

Другие предметы

2 года назад

в каком году начали играть футбол?

Русский язык

2 года назад

картофель(свариться).молоко(кипеть).сирень(расцвести). восток(заалеть).Мышь(пробежала).Такси(подъехать).ночь(пройти)месяц(светить).пальто(весеть).трактор(работать).составьте нераспространённые

История

7 лет назад

написати повідомлення про міста герої будь ласка (7-10 речень ) дам 100 балов

Математика

7 лет назад

стороны триугольника находятся в отношений 5 :4:3, периметр триугольника 132см чему равно самая кароткая сторона триугольника (в см)?

Математика

10 лет назад

найди значение числовых выражений (30 +20)-20 (50+30)-10 (40+50)-30 (60+30)-50 (20+70)-40 (30+40)-60

Математика

10 лет назад

Каждому участнику выстовки дали на подготовку 4 недели. Для того чтобы сделать эскизы, нужно на 6 дней меньше, чем на остальную работу. Сколько времени нужно на остальную работу?

Математика

10 лет назад

Найдите значение выражения, предварительно составив схему вычеслений: а) (55+14445:321)*(319-283); б) (48+1160:145)*27-12.

Обществознание

10 лет назад

Кто хочет разбогатеть в течение дня, будет повешен в течение года.