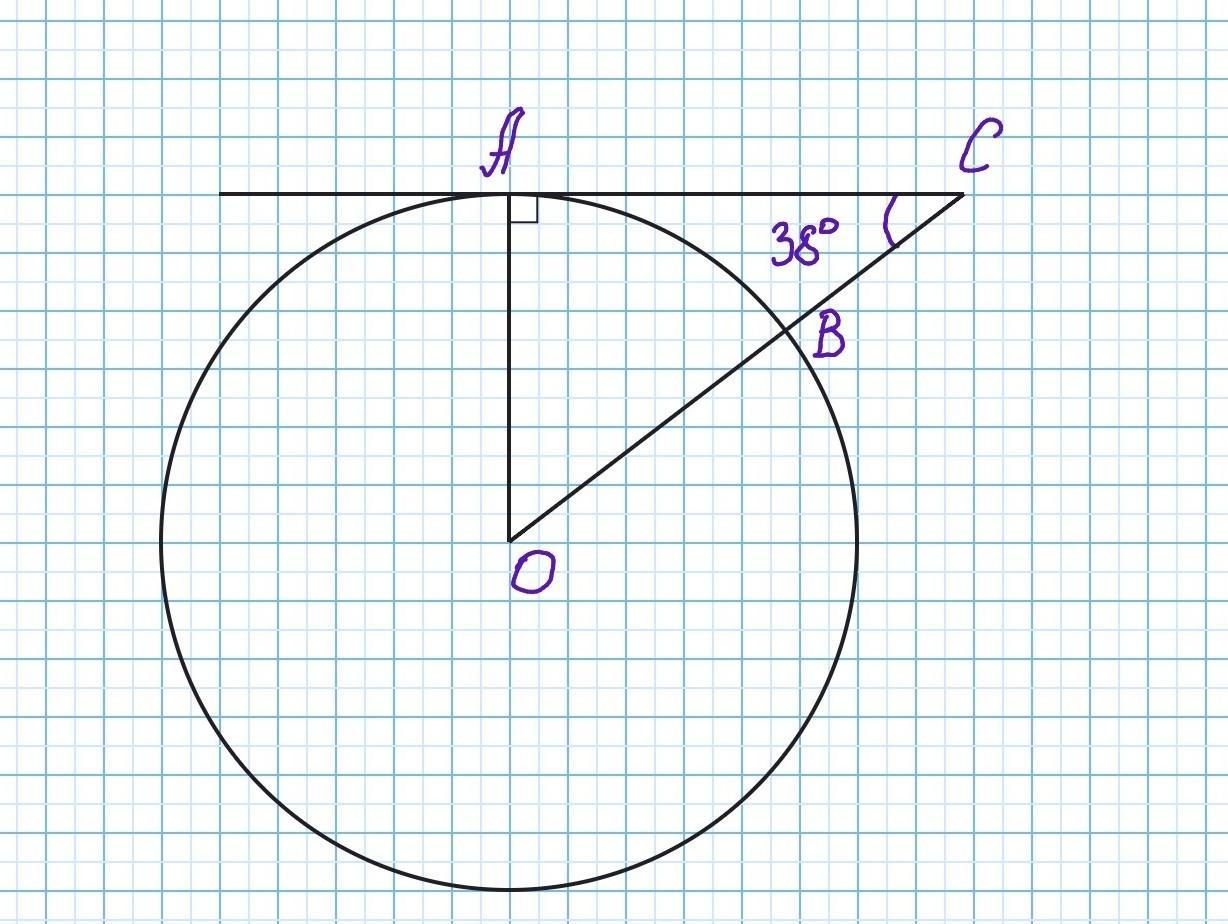
Угол ACB равен 38°. Его сторона CA касается окружности, сто-
рона СВ проходит через центр окружности. Найдите градусную
величину дуги АВ окружности, заключенной внутри этого угла
​

Ответ:

52°

Объяснение:

Сторона СА касается окружности. Значит СА перпендикулярна радиусу окружности.

СА⟂АО. Следовательно треугольник АОС - прямоугольный. По свойству острых углов прямоугольного треугольника ∠АОС=90°-∠АСО=90°-38°=52°

∠АОВ - центральный угол.

• Центральный угол — это угол, вершина которого лежит в центре окружности. 
• Центральный угол равен градусной мере дуги, на которую он опирается. 

∠АОВ опирается на дугу АВ, заключённую внутри угла АСВ.

Следовательно дуга АВ = 52°.