Помагите пожалуйста!!!!!

Приложения:

Ответы

Ответ дал: RayMiller

Ответ:

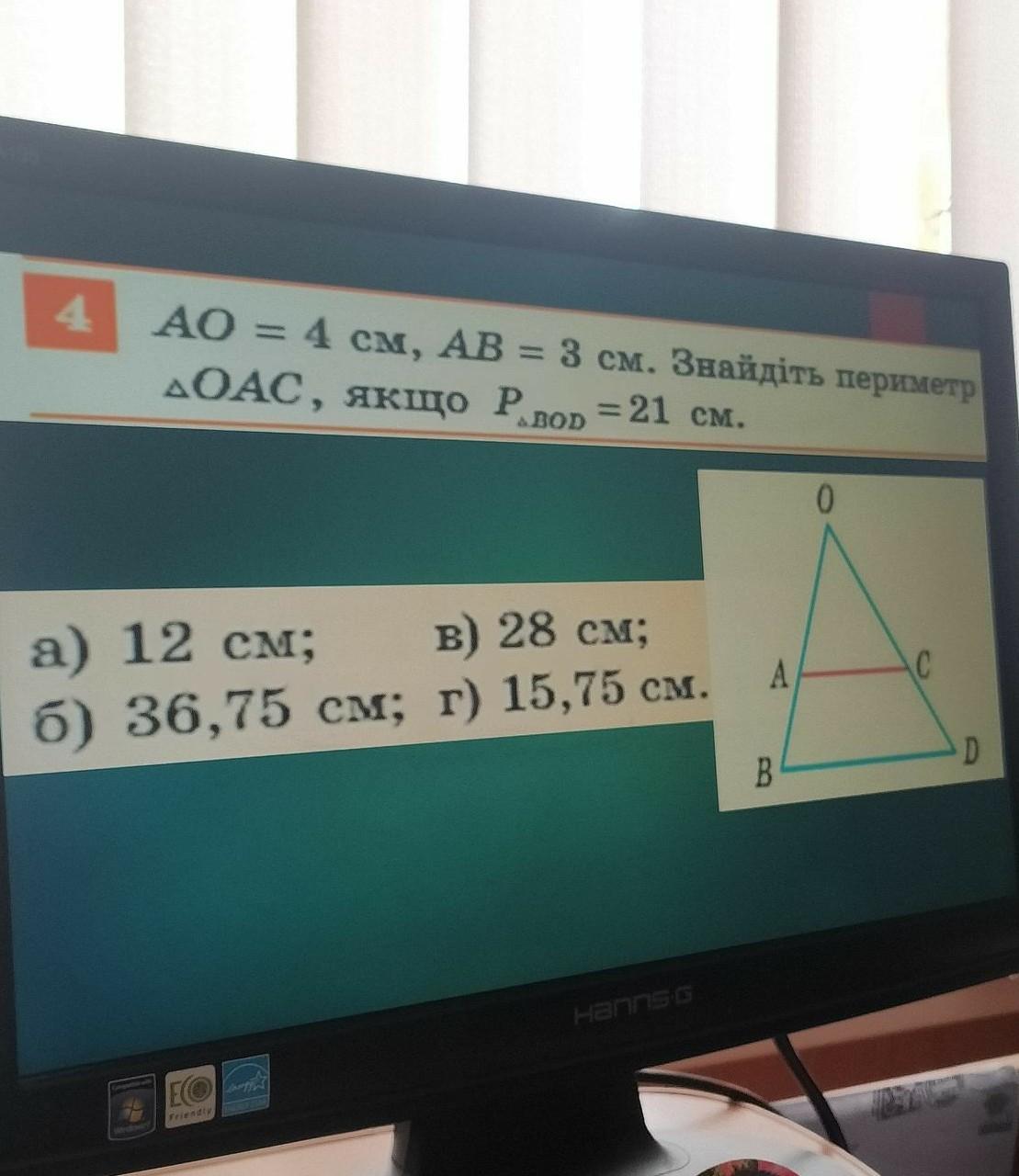
Предположительно в условии так же подразумевается, что AC || BD, иначе решить задание невозможно.

Решение:

Прямая, параллельная одной из сторон треугольника, отсекает от треугольника треугольник, подобный данному.

Так как АС||BD по условию, то ∆AOC~∆BOD.

$k = \frac{AO}{ BO} \\ k = \frac{AO}{AO + BA} \\ k = \frac{4}{4 + 3} \\ k = \frac{4}{7}$

Отношение периметров подобных треугольников равно коэффициенту подобия. То есть:

$\frac{P(AOC)}{P(BOD)} = \frac{4}{7} \\ \frac{P(AOC)}{21} = \frac{4}{7} \\ 7 \times P(AOC) = 4 \times 21 \\ P(AOC) = 4 \times 3 \\ P(AOC) = 12$

Ответ: 12 см.

Похожие вопросы

Русский язык

1 год назад

Английский язык

1 год назад

Русский язык

2 года назад

Другие предметы

2 года назад

Алгебра

7 лет назад

Как решить эту систему? $cos(x) cos(y) = frac{1}{4}$ $sin(x) sin(y) = frac{3}{4}$

Химия

7 лет назад

Алгебра

9 лет назад

Математика

9 лет назад