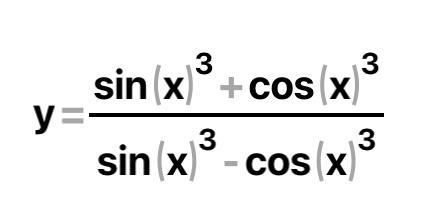Предмет: Алгебра
Автор: Пазенко
Вопрос задан 2 года назад

< >

Найти значение функции, если tg (x)=2

Приложения:

Ответы

Ответ дал: AlyaksandrK

1

Ответ: $\frac{9}{7}$

Объяснение: очень надеюсь, что это синусы и косинусы в степенях, а не значение Х. Умножим числитель и знаменатель на $\frac{1}{cos^{3}x }$ ;

$\frac{sin^{3}x+cos^{3}x }{sin^{3}x-cos^{3}x} =\frac{\frac{1}{cos^{3}x} (sin^{3}x+cos^{3}x) }{\frac{1}{cos^{3}x} (sin^{3}x-cos^{3}x)}=\frac{\frac{sin^{3}}{cos^{3}x} x+1}{\frac{sin^{3}x}{cos^{3}x} -1} =\frac{tg^{3}x+1 }{tg^{3}x-1} ;\\\frac{2^{3}+1 }{2^{3}-1 } =\frac{8+1}{8-1}=\frac{9}{7}$

Пазенко: Да, да это синусы и косинусы в степенях. Спасибо огромное)))

Похожие вопросы

Английский язык

1 год назад

переведите, пожалуйста!!!

Английский язык

1 год назад

Грамматика. Помогите, срочно нужно

Английский язык

2 года назад

I've got tickets for the Cup ...(вставить слово вместо пропуска. Слово состоит из 5 букв) You need a boat for this sport (ответить на вопрос. Ответ из 7 букв) I can't go swimming.I haven't got

Английский язык

2 года назад

переведи на английский язык.в левом углу,в правом углу,под кроватью,над столлм,за креслом,между диваном и пианоно,рядом с камином.

Математика

7 лет назад

Помогите пожалуйста прошу

История

7 лет назад

А яку роль відіграла Жанна д'Арк у Столітній війні ?

Алгебра

9 лет назад

Помогите сделать домашнюю работу по алгебре пожалуйста. Выполнить действия и записать результат в виде десятичной дроби: Желательно на листочке решить! срочно!!!! 1)2/11+1/9 2)8/13+2/3 3)1/3+1,25

История

9 лет назад

Мы уверяем ,что Юстиниан 1 Повлиял на историю Византий. Вопрос да или нет ? Почему Объясните Вывод