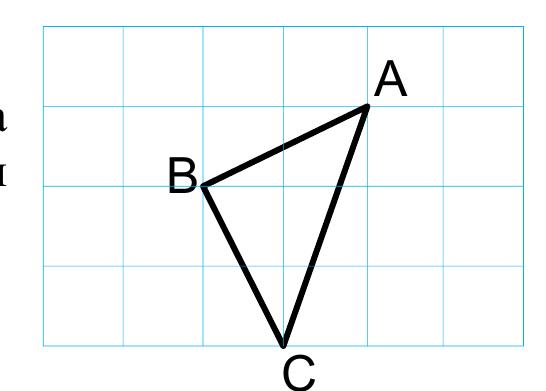
Найдите  высоту  треугольника  ABC,  опущенную  на
сторону  АС,  если  стороны  квадратных  клеток  равны
√10

В ΔАВС
АВ² = (√10)²+(2√10)²=50  ⇒ АВ=√50
ВС² = (√10)²+(2√10)²=50  ⇒ АВ=√50
АС² = ( (√10)²+(3√10)²=100  ⇒ АС=10

Высота проведенная к основанию АС делит ΔАВС на два равных прямоугольных треугольника с гипотенузой √50 и катетом 10:2=5
h² = (√50)² - (√25)²=25
h=5