найдите площадь АВС...

Ответ:

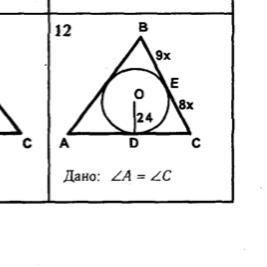
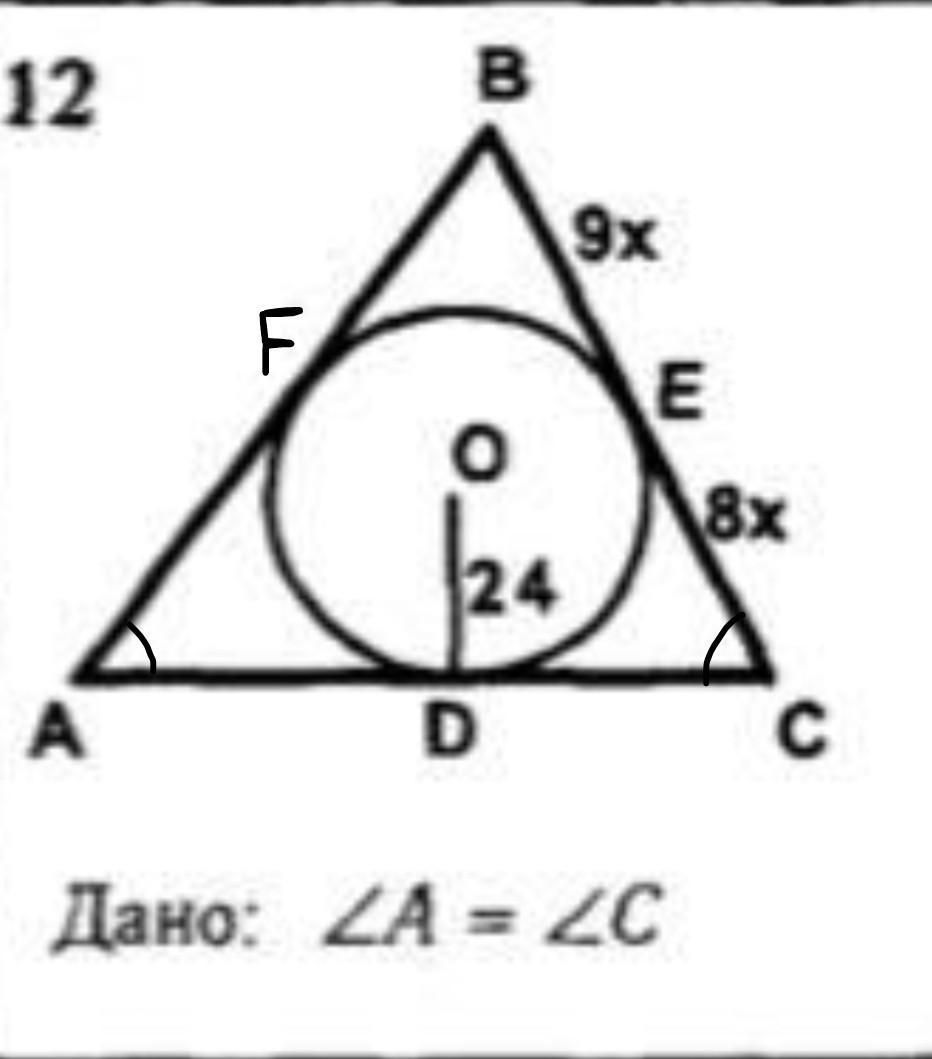
Дано:

В ∆АВС вписана окружность,

F, E, D – точки касания,

∠А=∠С,

OD – радиус вписанной окружности,

ОD=24

BE=9x,

EC=8x.

Решение:

Так как ∠ВАС=∠ВСА, то ∆АВС – равнобедренный с основанием АС. Значит ВА=ВС.

ВС=ВЕ+ЕС=9х+8х=17х, тогда ВА=17х также.

Отрезки касательных, проведённых из одной точки к окружности, равны. Следовательно:

BF=BE=9x, CD=CE=8x.

AF=BA–BF=17x–9x=8x

АС=AD+CD=8x+8x=16x.

Радиус вписанной в треугольник окружности можно найти по формуле:

где р – полупериметр треугольника.

Радиус OD вписанной окружности известен из условия. Подставим все известные значения в формулу:

Площадь треугольника равна произведению радиуса вписанной окружности и полупериметра треугольника.

p=25x=5*25=125.

OD=24 по условию

S=OD*p=24*125=3000.

Ответ: 3000