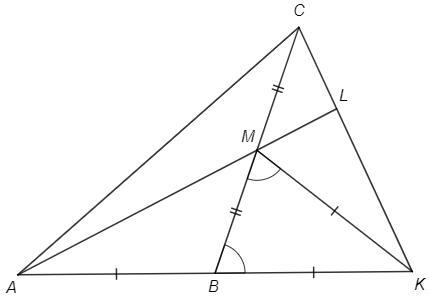
На продолжении стороны AB треугольника ABC за точку B отмечена точка K, такая что KB= AB. Продолжение медианы AM треугольника ABC за точку M пересекает отрезок CK в точке L. Оказалось, что KM = AB. Докажите, что ∠AMB= ∠KCB.
Если увидели не верный ответ, продолжайте решать, ответ скоро уберут:)
Ответы
Ответ дал:
19
AB=KB=KM
△BKM - равнобедренный, ∠KBM=∠KMB
∠ABM=∠KMC (смежные с равными)
△ABM=△KMC (по двум сторонам и углу между ними) => ∠AMB=∠KCM
Приложения:
Похожие вопросы
1 год назад
1 год назад
2 года назад
7 лет назад
7 лет назад