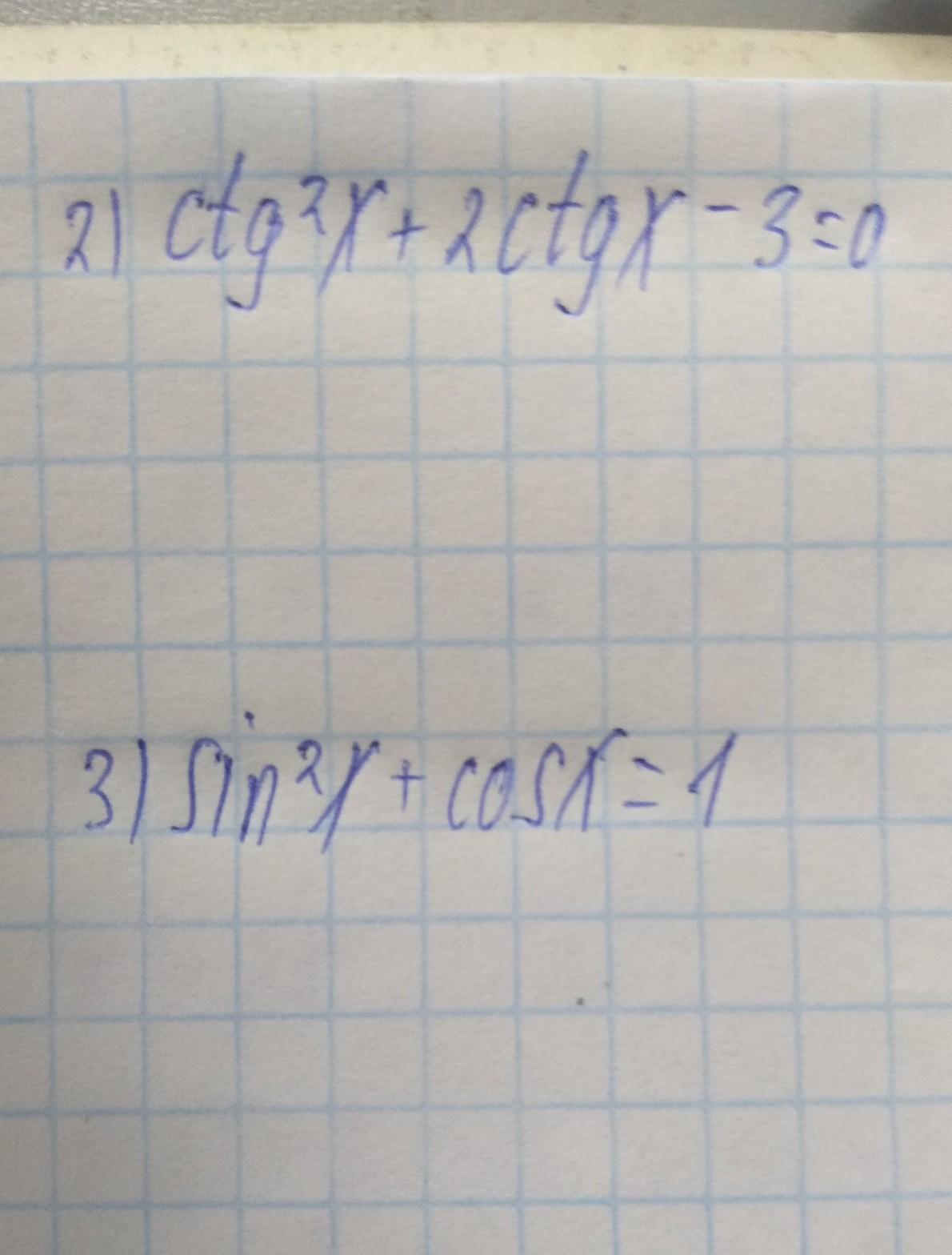• Предмет: Алгебра
  • Автор: kwinkl
  • Вопрос задан 2 года назад
< >

ПОМОГИТЕ хелпппппппп​

Приложения:
kwinkl: ПЖ
kwinkl: помогите

Ответы

Ответ дал: m11m
1

Ответ:

Объяснение:

!!!!!!!!!!!!!!!!!!!!!!!!!!!

Приложения:
Ответ дал: MatemaT123
0

Ответ:

x=\dfrac{\pi}{4}+\pi n, \quad n \in \mathbb {Z} \quad ; \quad x=\pi-arcctg3+\pi n, \quad n \in \mathbb {Z};

x=\pm \dfrac{\pi}{2}+2\pi n, \quad n \in \mathbb {Z} \quad ; \quad x=2\pi n, \quad n \in \mathbb {Z};

Объяснение:

2) \quad ctg^{2}x+2ctgx-3=0;

Введём замену:

t=ctgx;

Перепишем уравнение с учётом замены:

t^{2}+2t-3=0;

t^{2}+3t-t-3=0;

t(t+3)-1(t+3)=0;

(t-1)(t+3)=0;

t-1=0 \quad \vee \quad t+3=0;

t=1 \quad \vee \quad t=-3;

Вернёмся к замене:

ctgx=1 \quad \vee \quad ctgx=-3;

x=arcctg1+\pi n, \quad n \in \mathbb {Z} \quad \vee \quad x=arcctg(-3)+\pi n, \quad n \in \mathbb {Z};

x=\dfrac{\pi}{4}+\pi n, \quad n \in \mathbb {Z} \quad \vee \quad x=\pi-arcctg3+\pi n, \quad n \in \mathbb {Z};

3) \quad sin^{2}x+cosx=1;

1-cos^{2}x+cosx=1;

-cos^{2}x+cosx=1-1;

-cos^{2}+cosx=0 \quad | \quad \cdot (-1)

cos^{2}x-cosx=0;

cosx(cosx-1)=0;

cosx=0 \quad \vee \quad cosx-1=0;

x=\pm arccos0+2\pi n, \quad n \in \mathbb {Z} \quad \vee \quad cosx=1;

x=\pm \dfrac{\pi}{2}+2\pi n, \quad n \in \mathbb {Z} \quad \vee \quad x=\pm arccos1+2\pi n, \quad n \in \mathbb {Z};

x=\pm \dfrac{\pi}{2}+2\pi n, \quad n \in \mathbb {Z} \quad \vee \quad x=\pm 0+2\pi n, \quad n \in \mathbb {Z};

x=\pm \dfrac{\pi}{2}+2\pi n, \quad n \in \mathbb {Z} \quad \vee \quad x=2\pi n, \quad n \in \mathbb {Z};

Похожие вопросы
Українська література
1 год назад
«Васильки» В.Сосюри – це лірика: а) інтимна; б) пейзажна; в) філософська; г) громадянська.
Беларуская мова
1 год назад
Можете помочь. Нужно 10 предложений с синтаксическим разбором на белоруском. :) Жду.
Математика
2 года назад
во сколько раз произведение чисел 7164 и 48 больше разности чисел 1953 и 1921
Русский язык
2 года назад
Помогите раставить знаки припенания,пожалуйста. Пушкин самый любимой мною поэт.С каждым годом я воспринимаю его все больше и больше как гения страны,в которой я живу.Все это я рассказываю вам как
Математика
7 лет назад
помогите пожалуйста с дискретной математикой​
Алгебра
7 лет назад
Постройте график функции y=x+1
Литература
9 лет назад
Помогите пожалуйста сравнить сказки царевна лягушка и гуси лебеди, что в них общего и в чем отличие. Спасибо за ранее!
Математика
9 лет назад
Чтобы засеять льном 4 га , необходим 6 ц льняного семени. Сколько гектар можно засеять 450 кг льняного семенио