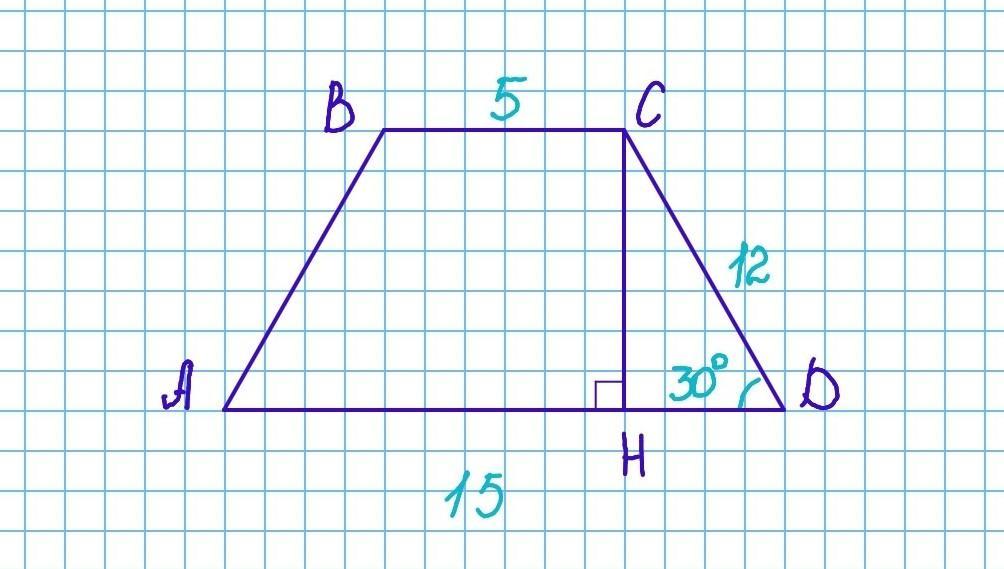
Основания трапеции равны 5 см и 15 см, а боковая сторона равная 12см
образует с одним из оснований трапеции угол равный 30° Найдите
площадь трапеции.​

Основания трапеции равны 5 см и 15 см, а боковая сторона равная 12см образует с одним из оснований трапеции угол равный 30°. Найдите площадь трапеции.

Ответ:

60 см²

Объяснение:

• Площадь трапеции равна произведению полусуммы её оснований на высоту.

Проведём высоту СН.

СН⟂AD, следовательно △CHD - прямоугольный. По условию гипотенуза CD=12см, а ∠D=30°.

• Напротив угла в 30° лежит катет, равный половине гипотенузы.

Поэтому СН = ½•CD = ½•12 = 6 см.

Тогда площадь трапеции:

Площадь трапеции равна 60 см²