Геометрия!!
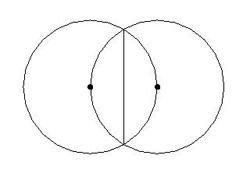
Одна из двух равных окружностей проходит через центр другой окружности.
Вычисли длину общей хорды, если радиус окружности равен 14 м.
Ответ: длина общей хорды равна
−−−−−√ м.
Приложения:
Ответы
Ответ дал:
5
Ответ:
14 корней из 3
Пошаговое объяснение:
Общая касательная и радиус этих окружностей перпендикулярны, и поэтому образуется прямоугольный треугольник с гипотенузой 14 и катетом 7, как половина радиуса. По теореме Пифагора находим, что половина общей хорды равна 7 корней из 3, а вся хорда - 14 корней из 3
Похожие вопросы
1 год назад
1 год назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад