Решите Пж 6-ШЕСТЬ треугольников. 100БАЛОВ!!!!!! Либо несколько СРОЧНО!!!

Приложения:

Ответы

Ответ дал: Аноним

6{1}.

Ответ: x = 7.94

Объяснение:

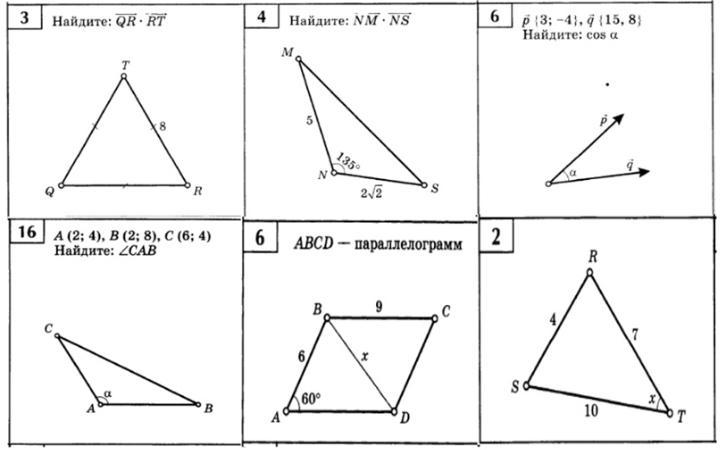
Так как ABC — параллолограмм, то AD == BC = 9; AB == CD = 6.

Тоесть в треугольнике ΔABD — нам звестно 2 стороны(AB & AD), и угол между ними(<A = 60°).

Чтобы найти третью сторону, или BD диагональ — используем теорему косинусов: $a = \sqrt{b^2+c^2-2bc*cos \gamma}$

Косинус гаммы: 0.5

$a = \sqrt{9^2+6^2-2*9*6*0.5}\\a = \sqrt{117-54} => a = \sqrt{63}\\a = 7.94 => BD = 7.94 => x = 7.94.$

Ответ: x = 18°

Объяснение:

Опять же, теорема косинусов, но в обратном порядке:

$cos\alpha = \frac{a^2+c^2-b^2}{2ac}\\cos\beta = \frac{a^2+b^2-c^2}{2ab}\\cos\gamma = \frac{b^2+c^2-a^2}{2cb}$

$cos(x) = \frac{7^2+10^2-4^2}{2*10*7}\\cos(x) = \frac{133}{140} => cos(x) = 0.95\\x = 18.19^o$

$cos(S) = \frac{4^2+10^2-7^2}{2*4*10}\\cos(S) = \frac{67}{80}\\cos(S) = 0.8375\\<S = 33.12^o$

$cos(<B) = \frac{4^2+7^2-10^2}{2*4*7}\\cos(<B) = \frac{-35}{56}\\cos(<B) = -0.625 => <B = 128.68^o$

128.68+33.12+18.19 = 179.99°.

Похожие вопросы

Қазақ тiлi

1 год назад

Другие предметы

1 год назад

Русский язык

2 года назад

Қазақ тiлi

2 года назад

Математика

7 лет назад

Алгебра

7 лет назад

Математика

9 лет назад

История

9 лет назад