через точку окружности радиуса r проведены касательная и хорда, равная r корень из 3. найдите угол между ними

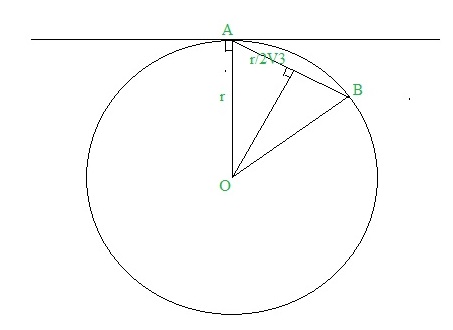
проведем из центра окружности 2 отрезка к окончаниям хорды и 1 отрезок к центру хорды, получим 2 прямоугольных треугольника.
рассмотрим тот, угол которого находится на касательной к окружности.
гипотенуза треугольника радиусу = r
катет = r / 2 √3
таким образом для угла через который проходит касательная:
sin (OAB) = катет / гипотенузу = r / 2 √3  / r = 1/2*√3
угол = 60 градусов
искомый угол = 90 - 60 = 30 градусов