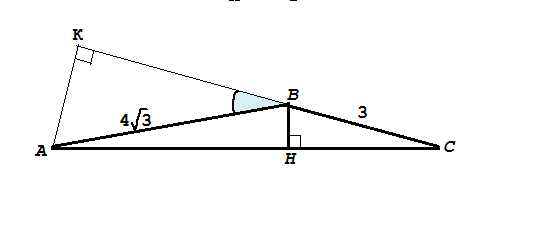
в треугольнике ABC AB=4 корней из 3, BC=3. площадь треугольника равна 3корня из 3. найдем высоту опущенную из вершины B если 90градусов<уголB<180градусов
Ответы
Ответ дал:
0
По условию 90º< угол В <180º, следовательно, этот угол тупой.
Площадь треугольника можно найти половиной произведения сторон, умноженной на синус угла между ними.
S ABC=AB*BC*sin∠B:2
3√3=4√3*3*sin∠B):2
1=2*sin∠B
sin∠B=1/2 - это синус 30º и 150º, но по условию угол В тупой, значит, он равен 150º
∠B=150º
Из вершины А проведем перпендикуляр к продолжению СВ до пересечения с ней в точке К.
Треугольник АКВ - прямоугольный, угол АВК смежный с углом АВС
угол АВК= 180º-150º=30º
КВ противолежит углу 60º. КВ=АВ*sin 60º
КВ=4√3*(√3):2=6
КС=КВ+ВС=9
АК противолежит углу 30º
АК=АВ*sin30º=4√3*0,5=2√3
По т. Пифагора гипотенуза прямоугольного треугольника АКС
АС²=АК²+КС²= 12+ 81=93
АС=√93=√31*√3
Площадь △АВС=АС*ВН:24√3= √31*√3*BH:2
8=√31*BH
ВН=8/√31
Площадь треугольника можно найти половиной произведения сторон, умноженной на синус угла между ними.
S ABC=AB*BC*sin∠B:2
3√3=4√3*3*sin∠B):2
1=2*sin∠B
sin∠B=1/2 - это синус 30º и 150º, но по условию угол В тупой, значит, он равен 150º
∠B=150º
Из вершины А проведем перпендикуляр к продолжению СВ до пересечения с ней в точке К.
Треугольник АКВ - прямоугольный, угол АВК смежный с углом АВС
угол АВК= 180º-150º=30º
КВ противолежит углу 60º. КВ=АВ*sin 60º
КВ=4√3*(√3):2=6
КС=КВ+ВС=9
АК противолежит углу 30º
АК=АВ*sin30º=4√3*0,5=2√3
По т. Пифагора гипотенуза прямоугольного треугольника АКС
АС²=АК²+КС²= 12+ 81=93
АС=√93=√31*√3
Площадь △АВС=АС*ВН:24√3= √31*√3*BH:2
8=√31*BH
ВН=8/√31
Приложения:
Похожие вопросы
2 года назад
2 года назад
7 лет назад
10 лет назад