З точки до прямої проведено дві похилі, проекції яких на цю пряму дорівнюють 5 см і 9 см. Знайти довжини похилих, якщо їх сума дорівнює 28см

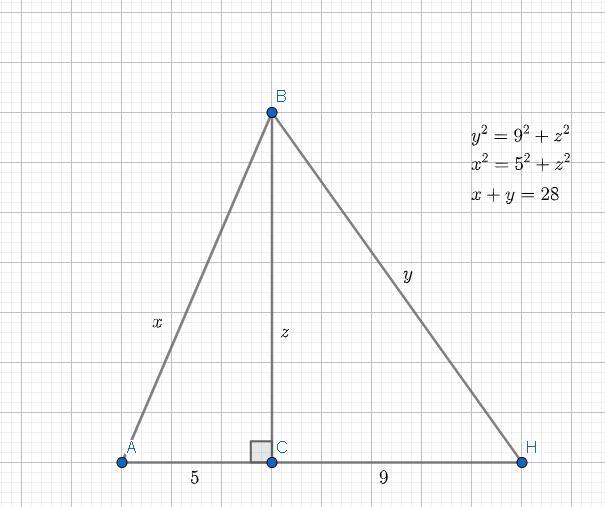
Построем 2 наклонные, проведённые с одной точки до прямой.

Список наклонных: BH; AB.

Проекция наклонной BH — это отрезок CH.

Проекция наклонной AB — AC.

По теореме Пифагора, наклонную можем найти, зная 2 катета, тоесть:

Объявим неизвестные числа как переменные: AB = x; BC = z; BH = y.

У нас есть 2 условия, они таковы:

Но в задании ещё задано третье условие! Что сумма наклонных равна 28см, тоесть третье условие таково:

Составим трёхрядную систему:

Вывод: BH = 15; AB = 13.