Предмет: Математика
Автор: moldirotar
Вопрос задан 2 года назад

< >

Вычислить двойной интеграл

Приложения:

Ответы

Ответ дал: NNNLLL54

1

Ответ:

$\iint \limits _{D}\, \sqrt{xy}\, dx\, dy=\int\limits^4_1\, dx\int\limits_0^1\, \sqrt{xy}\, dy=\int\limits^4_1\, dx\int\limits_0^1\, \sqrt{x}\cdot \sqrt{y}\, dy=\int\limits^4_1\, \sqrt{x}\, dx\int\limits_0^1\, \sqrt{y}\, dy=\\\\\\=\int\limits^4_1\, \sqrt{x}\, dx\, \Big(\dfrac{2\, y^{\frac{3}{2}}}{3}\Big)\Big|_0^1=\int\limits^4_1\, \sqrt{x}\cdot\dfrac{2}{3}\, dx=\dfrac{2}{3}\cdot \dfrac{2\, x^{\frac{3}{2}}}{3}\, \Big|_1^4=\dfrac{4}{9}\cdot \Big(4^{\frac{3}{2}}-1^{\frac{3}{2}}\Big)=$

$=\dfrac{4}{9}\cdot \Big(\sqrt{4^3}-1\Big)=\dfrac{4}{9}\cdot \Big(\sqrt{4^2\cdot 4}-1\Big)=\dfrac{4}{9}\cdot \Big(4\cdot 2-1\Big)=\dfrac{4}{9}\cdot7=\dfrac{28}{9}$

Приложения:

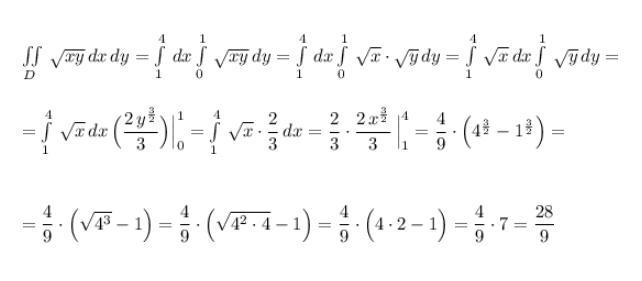
moldirotar: Здравствуйте,можете ссылку скинуть или фото заново,тут не полностью видно,пожалуйстаа))

NNNLLL54: фото добавила

moldirotar: Спасибо вам огромное)

Похожие вопросы

Английский язык

1 год назад

Read the word combination and give their Russian eguivalents:The story told by Granny, the picture taken in London, mistakes made in the test, the present bought for my brother, dinners cooked by

Немецкий язык

1 год назад

Упражнение 1. Перепишите предложения и переведите только те, действие которых происходит в настоящее время: 1. Die Einwohnerzahl der Bundesrepublik wird bis zum Jahr 2030 auf ca. 48 Millionen

Русский язык

2 года назад

составь два предложения употребив в них одно из данных имён существительных сначала в форме именительного падежа затем в форме винительного падежа запишите предложения слова: книга площадь учитель

Английский язык

2 года назад

помогите прочитать эти слова по because, wrong, but, snow, sun, is, only.спасибо

Биология

7 лет назад

Помогите решить 3 и 4 вопрос Люди ПОЖАЛУЙСТА

Математика

7 лет назад

ABCD прямоугольник AC=12 см CD=8 см . Найдите периметр треугольника АОВ, где О точка пересечения диагоналей

Алгебра

9 лет назад

Как решить пример -3,28+1,75

Математика

9 лет назад

решение пределов,ответ минимум из 2-х решений