Все вершины квадрата лежат на координатных осях. Ордината одной из вершин равна 3. Укажи на рисунке все вершины и найди площадь квадрата.
Ответ: кв.ед.

Ответ:

квадратных единиц

Смотрите рисунок!

Объяснение:

Смотрите рисунок!

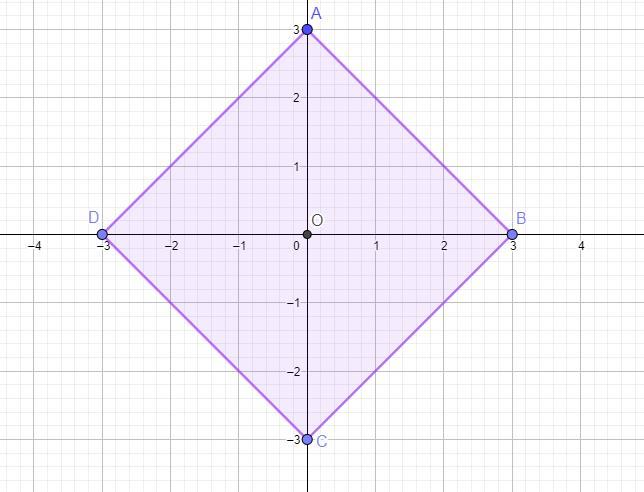
Пусть точка ордината которой 3 - точка A, тогда координаты точки A(0;3), пусть остальные точки квадрата которые лежат на координатных осях это точки B,C,D. Из-за симметрии квадрат координаты этих точек:

B(3;0), C(0;-3), D(-3;0). Найдем длину отрезка AB по формуле длинны отрезка между двумя точками:

По формуле площади квадрата квадратных единиц.