Предмет: Алгебра
Автор: Аноним
Вопрос задан 2 года назад

< >

Решите 2-4 СРОЧНООООООООООООООООООООООООООООО

Приложения:

Ответы

Ответ дал: NNNLLL54

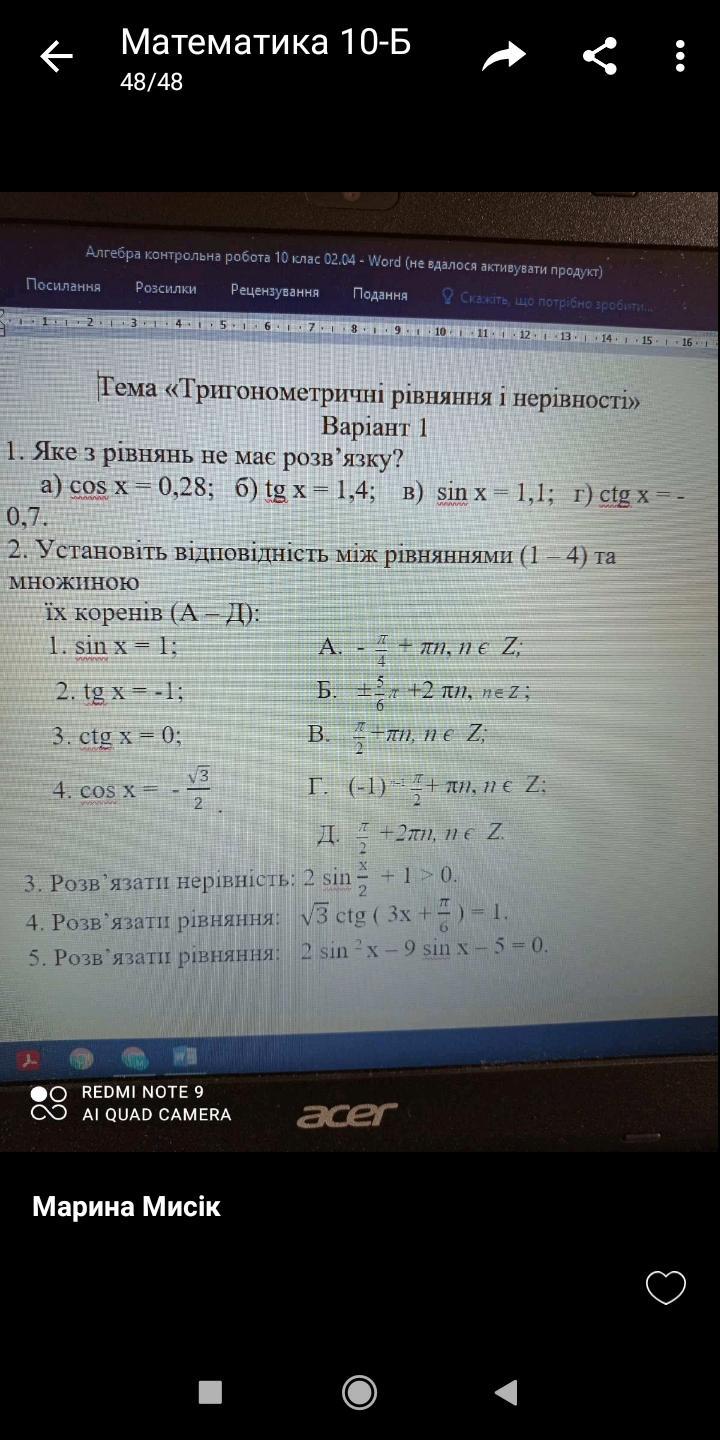
1

Ответ.

$1)\ \ sinx=1,1$ не имеет решений, так как $|sinx|\leq 1\ .$

2) 1 - Д , 2 - А , 3 - В , 4 - Б

$3)\ \ 2sin\dfrac{x}{2}+1>0\ \ \ \to \ \ sin\dfrac{x}{2}>-\dfrac{1}{2}\\\\\\-\dfrac{\pi }{6}+2\pi n<\dfrac{x}{2}<\dfrac{7\pi}{6}+2\pi n\ ,\ \ \ -\dfrac{\pi}{3}+4\pi n<x<\dfrac{7\pi}{3}+4\pi n\ ,\ n\in Z$

$4)\ \ \sqrt3ctg(3x+\frac{\pi}{6})=1\ \ \ \to \ \ \ ctg(3x+\frac{\pi}{6})=\dfrac{1}{\sqrt3}\ ,\\\\\\3x+\dfrac{\pi}{6}=\dfrac{\pi}{3}+\pi n\ \ ,\ \ \ 3x=\dfrac{\pi}{6}+\pi n\ \ ,\ \ x=\dfrac{\pi}{18}+\dfrac{\pi n}{3}\ \ ,\ n\in Z\\\\\\5)\ \ 2sin^2x-9sinx-5=0\ \ ,\ \ D=121\ \ ,\\\\a)\ \ sinx=\dfrac{9-11}{4}\ \ ,\ \ sinx=-\dfrac{1}{2}\ \ ,\ \ x=(-1)^{n+1}\cdot \dfrac{\pi}{6}+\pi n\ ,\ n\in Z\\\\b)\ \ sinx=5\ \ ,\ \ x\in \varnothing \\\\Otvet:\ x=(-1)^{n+1}\cdot \dfrac{\pi}{6}+\pi n\ ,\ n\in Z\ .$

Аноним: 3) Запишите уравнение прямой, которая является осью симметрии для перевода точки А(3-1,3) в точку А1(3-9;3)

Аноним: 4) Найдите координаты точки, симметричной точке А (3;3-4) относительно прямой, содержит биссектрисы 1 и 3 координатных углов.

Аноним: 5) Параллельный перенос задано формулами: х1=х+2 ,у1=в-2. Указать координаты точки в которую перейдет точка (3-6;3).

Аноним: 6) Укажите координаты точки, симметричной точке (3-7;3) относительно начала координат.

Аноним: 7) Найти координаты точки симметричной т.А(3,3-2) относительно т.В(3+2;3-3)

NNNLLL54: создай вопрос..... в комментариях не отвечают ....

NNNLLL54: кстати, более 3-х примеров нельзя размещать в вопросе ...

Аноним: я не могу создать вопрос

Аноним: пожалуйста помоги очень срочно нужно

Аноним: ты поможешь ?будь ласка

Похожие вопросы

Русский язык

1 год назад

сост диалог между ...

Русский язык

1 год назад

пожалуйста сочинение на тему "Мой любимый предмет"

Українська мова

2 года назад

звукова схема слова юрась

Русский язык

2 года назад

Выписать "глагол+сущ.,, В Косвенном падеже Витя предлагает Яне яблоко

География

7 лет назад

напишите все горы и равнины (в паинте например) на двух оборотах

Информатика

7 лет назад

Помогите пожалуйстадаю 30 баллов

Математика

9 лет назад

Длина прямоугольника равна 12 сантиметров ширина составляет 1 4 часть длины Найди периметр прямоугольника

Геометрия

9 лет назад

властивість медіаниани рівнобедреного трикутника проведеного до основи