стороны треугольника ABC равны 13, 14, 15. О - точка пересечения медиан. найдите площадь треугольника AOB
Ответы
Ответ дал:
0
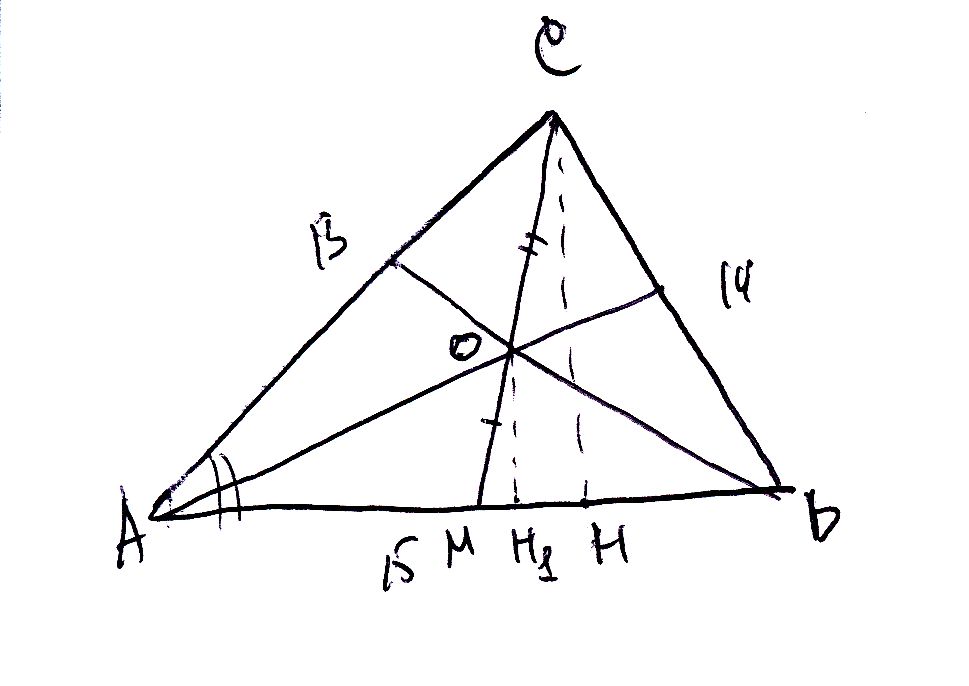
Смотри рисунок.
Из подобия MOH1 и MCH следует OH1 = 1/3*CH
Поэтому
S (AOB) = 1/3 * S (ABC)
CH = 13*sinA (A - угол при вершине А);
S (ABC) = 13*15*sinA/2;
15^2+13^2-2*13*15*cosA = 14^2 (теорема косинусов);
осюда cosA = 198/390; sinA = 336/390 = 56/65;
S (ABC) = 84; S (AOB) = 28.
Приложения:
Похожие вопросы
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад