Помогите пожалуйста. С теоремой. ​

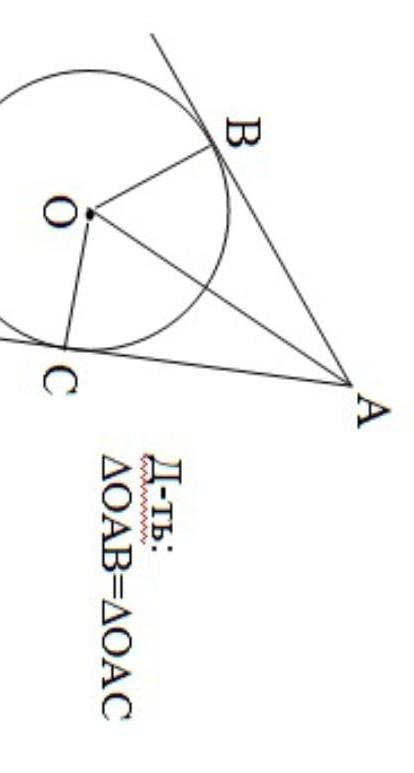
∆ОАВ и ∆ОАС - прямоугольные, поскольку касательные (возможно не правильно перевела с украинского "дотична") перпендикулярны к радиусам круга в точках B и C.

Сторона OA - общая.

Катеты OB = OC как радиусы одного и того же круга.

Треугольники равны за гипотенузой и катетом, отсюда равны и катеты AB и AC, а также углы BAO и CAO, то есть OA делит угол пополам.

Ответ: ∆ОАВ=∆ОАС