Дан квадрат ABCD и точка K на продолжении стороны AB за точку A такая, что A — середина отрезка KB. Точка L выбрана таким образом, что DL = CD, а угол BLK = 90◦. Чему может быть равен угол AKL? *
Ответы
Ответ дал:
7
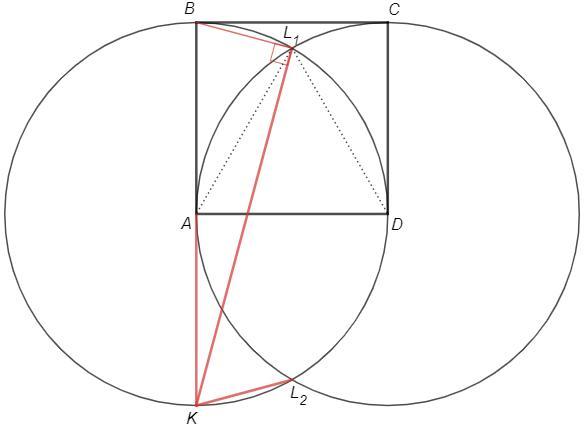
Точка L лежит на окружности с центром D радиусом CD (DL=CD, ГМТ удаленных от данной точки на радиус).
Точка L лежит на окружности с центром A диаметром BK (BLK=90, ГМТ из которых диаметр виден под прямым углом).
Окружности пересекаются в точках L1 и L2.
1) △AL1D - равносторонний (радиусы окружностей равны стороне квадрата), L1AD=60
BAL1 =90-60 =30
AKL1 =BKL1 =BAL1/2 =15° (вписанный равен половине центрального, опирающегося на ту же дугу)
2) Точки L1 и L2 симметричны относительно AD (по построению) => ∠BKL2=∠KBL1
AKL2 =KBL1 =90-BKL1 =90-15 =75°
Приложения:
Похожие вопросы
1 год назад
1 год назад
2 года назад
7 лет назад
7 лет назад
9 лет назад