віддаю останні бали.. пжпжпжпжпж хелп..​

1.

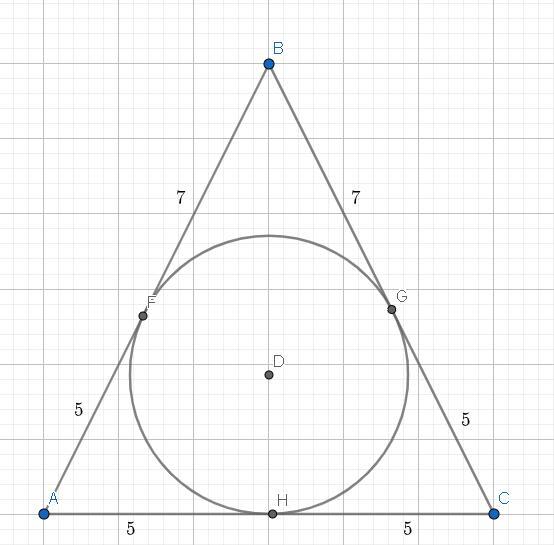
Так как окружность вписана в равнобедеренный треугольник, то все стороны — являются касательными окружности.

Заметим, что через точку B — проведены касательные BA & BC.

Теорема о касательных такова: 2 касательные, проведённые с одной точки, в точках касания  — равны друг другу.

То есть: BF == BG = 7 см (так как боковая сторона была разделена на отрезки 7 см & 5 см).

Одно и то же с отрезками AF & AH: AF == AH = 5.

И так как боковые стороны равны, то: GC == HC = 5 см.

AH == HC = 5 ⇒ AC = 5+5 = 10 см.

Следовательно:

Вывод: P = 34 см.