Предмет: Алгебра
Автор: Novaya22
Вопрос задан 2 года назад

100 баллов! срочно! С подробным пошаговым решением!

Приложения:

Ответы

Ответ дал: mionkaf1

$\displaystyle\\2)\ a) \int\limits^1_{-1} {e^x} \, dx=e^x\bigg | ^1_{-1}=e^1-e^{-1}=e-\frac{1}{e}\\\\b) \int\limits^{-1}_{-2} {-2x-x^2} \, dx =-x^2-\frac{x^3}{3}\bigg |^{-1}_{-2}=-(-1)^2-\frac{(-1)^3}{3}-\bigg(-(-2)^3-\frac{(-2)^3}{3} \bigg)=\\\\\\=\frac{2}{3}$

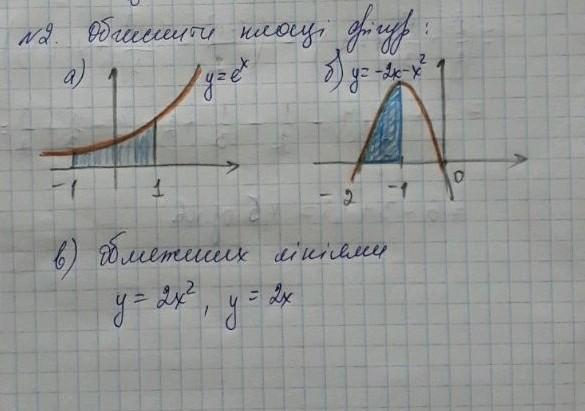
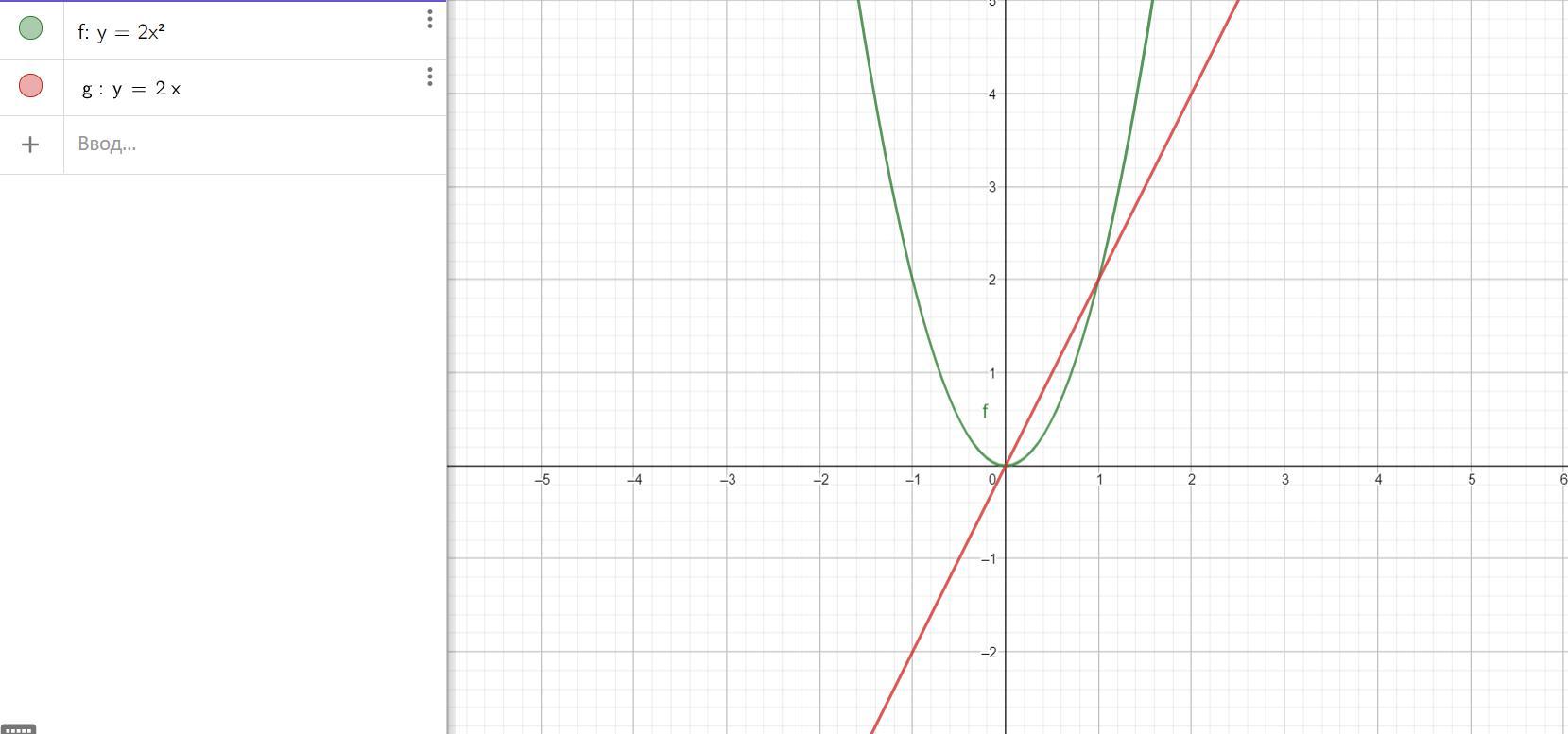
Построим графики (фото):

$\displaystyle\\\int\limits^1_0 {2x-2x^2} \, dx=x^2-\frac{2x^3}{3}\bigg |^1_0=1^2-\frac{2*1^3}{3}=1-\frac{2}{3}=\frac{1}{3}$

Приложения:

Lidagirl: Плиз помоги мне тоже

Novaya22: как в б вышло 2/3. более подробно распишите

Novaya22: сколько будет в а? нужен числовой ответ

mionkaf1: 1) 2/3 вышло если посчитать что идёт до 2/3 2) точного числового ответа нет, e это константа которая примерно равна 2,7, но в реальности намного больше цифр после запятой

Novaya22: распишите б, чтоб общий знаменатель и так далее, а не просто ответ.

Novaya22: и в распишите таблицей, чему равны х и у, чтоб построить графики

Похожие вопросы

Другие предметы

1 год назад

(1) Что делать, если вы пострадали соседом? (2) Что делать, если знакомый друг кричит? 3) Какого персонажа вы не любите? Что делать? 4) Какие отношения вы знаете о казахах? 5) Ваш друг не стоит в

Русский язык

1 год назад

Помагите пожайлуста написать сочинение .Как я живу в городе горловка поселок комарова улица шашурина дом 27 чем славится мой дом и как я горжусь своим поселком .

Английский язык

2 года назад

Read the sentences and say if they are true(T) or false (F) . 1.Liza in going to visit the Russian Museum. 2.Liza has tasted St Petersburg`s ice cream. 3.Liza likes being in St Petersburg. 4.She