Площадь сечения шара плоскостью равна 20 п , а расстояние от центра шара до секущей плоскости равно 4. Найти обьем шара
Ответы
Ответ дал:
0
S=pi*r^2
r^2=S/pi
R=корень(L^2+r^2)=корень(L^2+S/pi)
V=4/3*pi*R^3=4/3*pi*(L^2+S/pi)^(3/2)=4/3*pi*(4^2+20*pi/pi)^(3/2)=288*pi ~ 904,77868
r^2=S/pi
R=корень(L^2+r^2)=корень(L^2+S/pi)
V=4/3*pi*R^3=4/3*pi*(L^2+S/pi)^(3/2)=4/3*pi*(4^2+20*pi/pi)^(3/2)=288*pi ~ 904,77868
Ответ дал:
0
а нарушение за что !!!
Ответ дал:
0
???
Ответ дал:
0
так то
Ответ дал:
0
может пожаловаться на Вас ? или Вы извинитесь ?
Ответ дал:
0
02:05 mirok1 отметил нарушение в решении Пользователя IUV
02:01 mirok1 поблагодарил ВАС (т.е. меня) за решение
01:55 IUV добавил решение
01:42 mirok1 добавил задачу
02:01 mirok1 поблагодарил ВАС (т.е. меня) за решение
01:55 IUV добавил решение
01:42 mirok1 добавил задачу
Ответ дал:
0
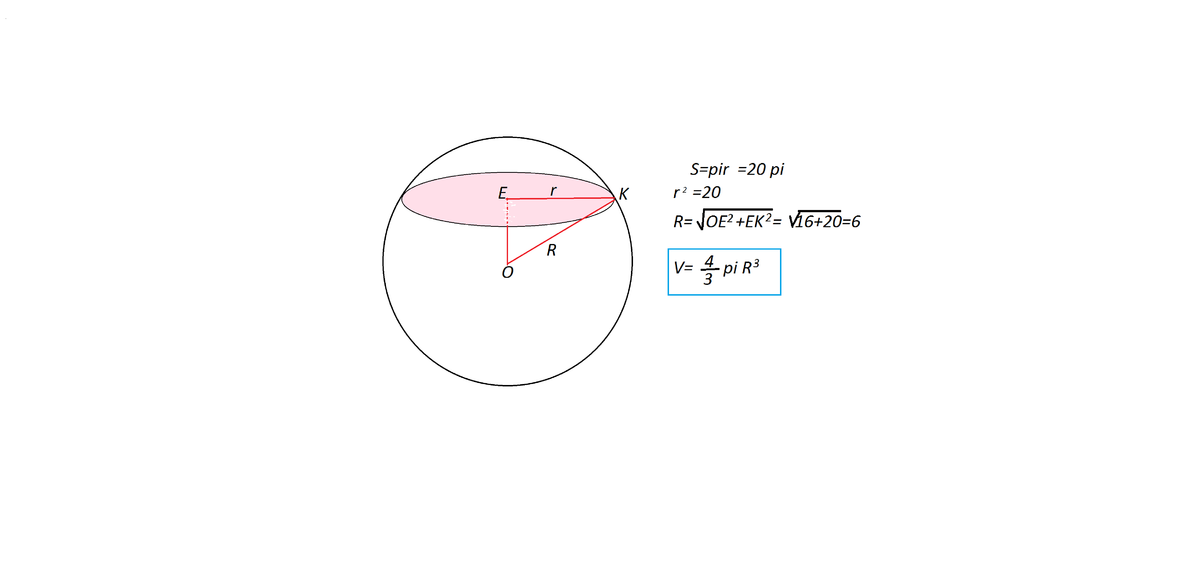
Сечение с центром Е находится на расстоянии 4 см от центра О шара.
Площадь сечения 20π
Объем шара найдем по формуле
V=(4πR³):3
Сделаем рисунок к задаче.
ОЕ - расстояние от центра шара до сечения,
r- радиус сечения,
R - радиус шара.
Треугольник ОЕК - прямоугольный, т.к. расстояние измеряется перпендикуляром, и ОЕ перпендикулярен ЕК.
R найдем по т.Пифагора. Он равен 6
V=4π*216:3=288π
Площадь сечения 20π
Объем шара найдем по формуле
V=(4πR³):3
Сделаем рисунок к задаче.
ОЕ - расстояние от центра шара до сечения,
r- радиус сечения,
R - радиус шара.
Треугольник ОЕК - прямоугольный, т.к. расстояние измеряется перпендикуляром, и ОЕ перпендикулярен ЕК.
R найдем по т.Пифагора. Он равен 6
V=4π*216:3=288π
Приложения:
Похожие вопросы
2 года назад
2 года назад
7 лет назад
10 лет назад
10 лет назад