Предмет: Математика
Автор: sergeevn801
Вопрос задан 2 года назад

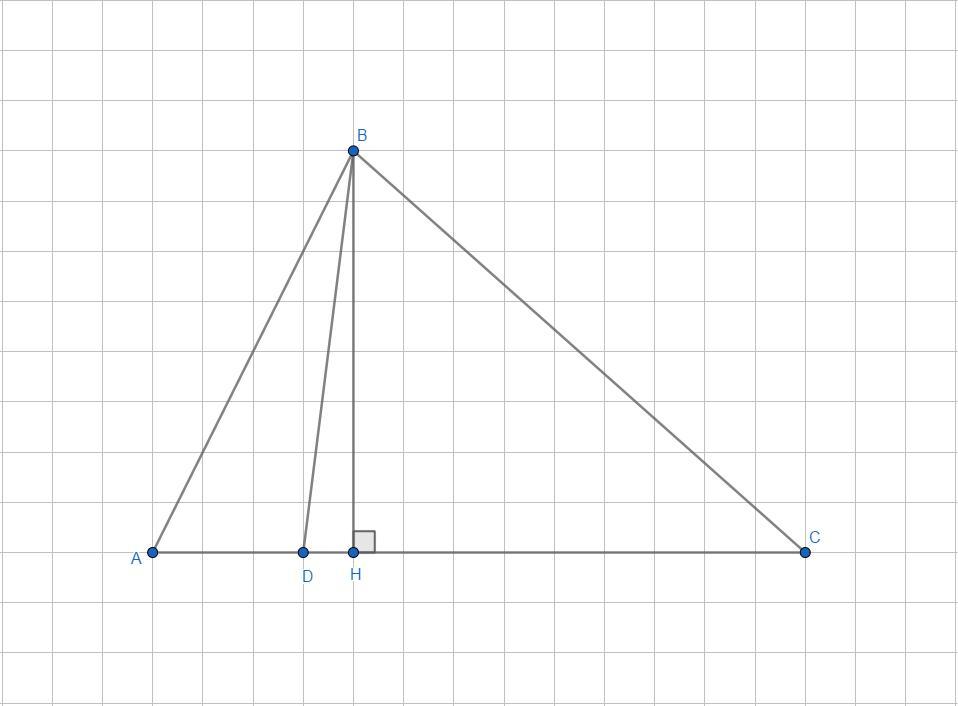
Дан треугольник ABC, на стороне AC которого взята точка D такая, что AD=5 см, а DC=17 см. Отрезок DB делит треугольник ABC на два треугольника. При этом площадь треугольника ABC составляет 154 см2.
Найди площадь меньшего из образовавшихся треугольников, ответ дай в квадратных сантиметрах.

Ответы

Ответ дал: Reideen

Ответ:

Площадь меньшего треугольника равна 35 см²

Объяснение:

Площадь треугольника находится по формуле: $\displaystyle \boldsymbol {S=\frac{1}{2}ah }$ , где a - сторона треугольника, h - высота, проведенная к этой стороне.

Найдем высоту треугольника ΔABC, зная его площадь и длину основания: $\displaystyle S_{\triangle ABC}=\frac{1}{2}\cdot BH\cdot AC$ , откуда $\displaystyle \boldsymbol{BH}=\frac{2 \cdot S_{\triangle ABC}}{AC} =\frac{2 \cdot S_{\triangle ABC}}{AD+DC}=\frac{2\cdot 154}{5+17}=\boldsymbol{14}$ см.

Высота BH треугольника ΔABC также является высотой треугольников ΔABD и ΔDBC, тогда можем найти их площади:

$\displaystyle \boldsymbol{S_{\triangle ABD}}=\frac{1}{2} \cdot AD \cdot BH=\frac{1}{2} \cdot 5\cdot 14=\boldsymbol{35 }$ см²;

$\displaystyle \boldsymbol{S_{\triangle DBC}}=\frac{1}{2} \cdot DC \cdot BH=\frac{1}{2} \cdot 17\cdot 14=\boldsymbol{119}$ см².

Итак, площади образовавшихся треугольников: $\displaystyle \boldsymbol{S_{\triangle ABD}}=\boldsymbol{35 }$ см² и $\displaystyle \boldsymbol{S_{\triangle DBC}}=\boldsymbol{119}$ см², значит, $\displaystyle \boldsymbol{S_{\triangle ABD}}<\boldsymbol{S_{\triangle DBC}}$ .