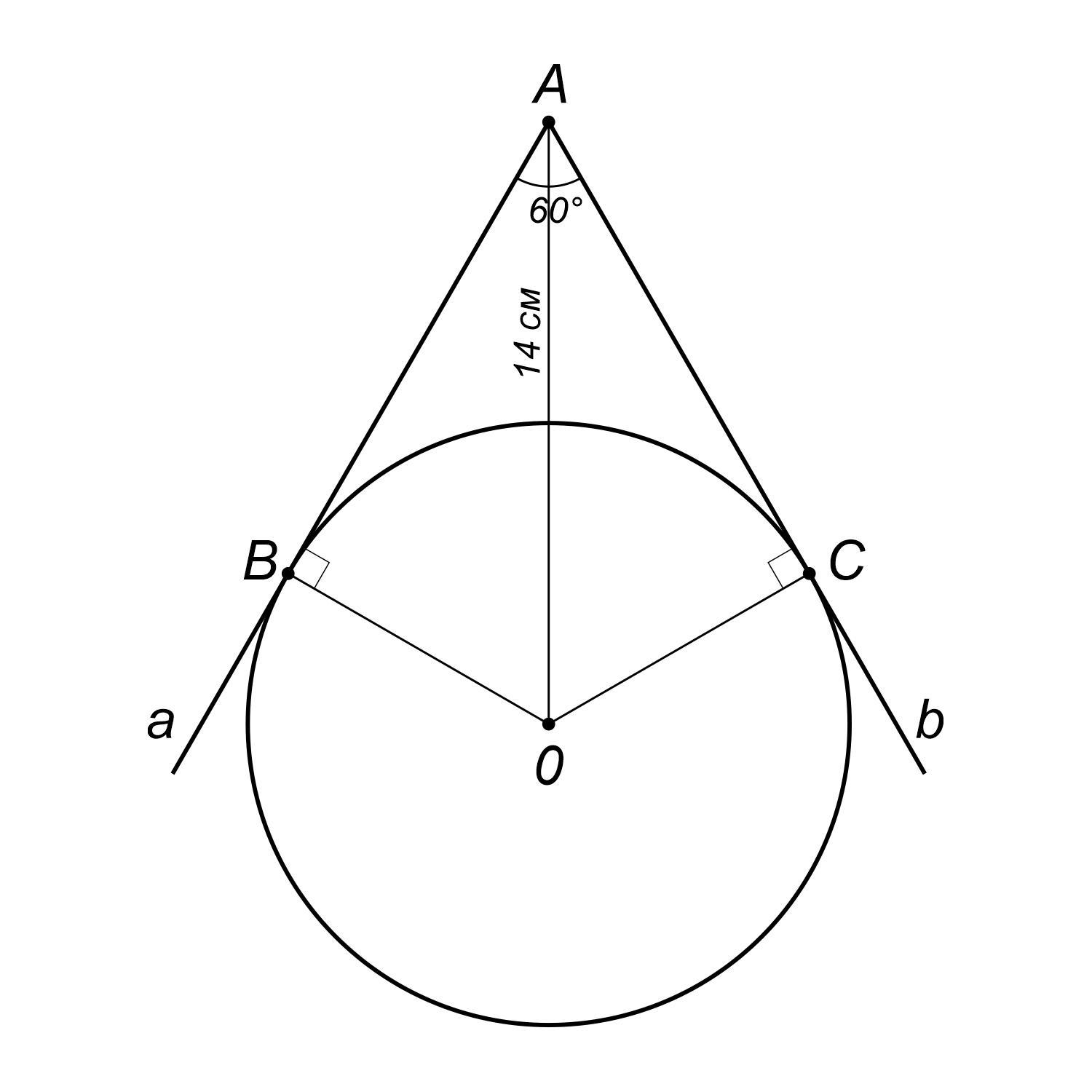
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равен 14см.
срочно!!!!!!!​

Ответ:

Радиус окружности = 7 см.

Объяснение:

Есть такая теорема: Если из какой-нибудь точки провести две касательные к окружности, то их отрезки от данной точки до точек касания равны между собой ⇒ AB = AC, и центр окружности находится на биссектрисе угла, образованного этими касательными ⇒ AO - биссектрисе угла ∠BAC.

⇒ ∠OAC = ∠OAB = ∠BAC/2 = 60°/2 = 30°

Также мы знаем что любая касательная к окружности перпендикулярна к его радиусу ⇒ ∠OCA = 90°.

Рассмотрим Δ OAC - это прямоугольный треугольник, гипотенуза которого AO = 14 см, а ∠OAC = 30°

Возьмём Синус угла ∠OAC - это отношение противолежащего этому углу катета к гипотенузе:

Зная что sin 30° = 1/2, a AC = 14 см, подставляем эти значения в формулу и вычисляем противолежащий катет OC (который по совместительству является и радиусом нашей окружности):