пожалуйста, очень нужно
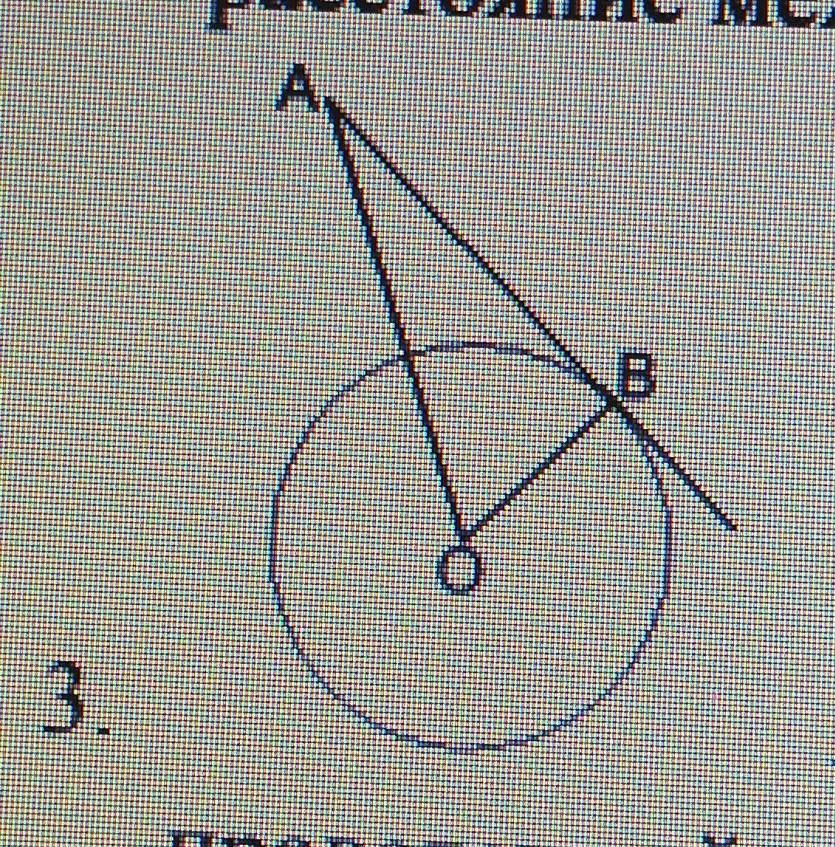
AB касательная к окружности с центром в точке O. OB- радиус,
проведенный в точку касания. Определите вид ∆AOB. ∟OAB = 300 , диаметр
окружности 10см. Найдите OA.
Приложения:
ademamarabayeva1:
там 30 граудусов
Ответы
Ответ дал:
1
Ответ:Если у вас нет значка «градусы»,то пишите слово буквами,а то в задании угол равен 300 градусов!!
Решение
Радиус ОВ является перпендикуляром к касательной АВ,поэтому
<АВО=90 градусов,а треугольник прямоугольный
Радиус ОВ равен половине диаметра
ОВ=10:2=5 см
По условию задачи угол ОАВ равен 30 градусов,катет ОВ лежит против этого угла,а значит равен половине гипотенузы,следовательно
ОА=5•2=10 см
Объяснение:
извиняюсь, за ошибку там 30°
спасибо огромное, вы спасли мне мою шкуру
Задача легкая
удачи
Похожие вопросы
1 год назад
2 года назад
7 лет назад
9 лет назад