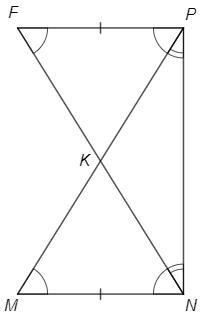
Гипотенузы МР и NF прямоугольных треугольников MNP и FPN пересекаются в точке К. MN = FP. Докажите, что:


а) треугольник NKP равнобедренный;


б) треугольник MNK равен треугольнику FPK.

MN=FP, PN - общий катет

△MNP=△FPN (по двум катетам)

∠M=∠F, ∠MPN=∠FNP

a)

∠MPN=∠FNP => ∠KPN=∠KNP

△NKP - равнобедренный (по признаку: углы при основании равны)

б)

Сумма острых углов прямоугольного треугольника 90.

∠KPF =90-∠MPN =∠M

∠KNM =90-∠FNP =∠F

∠KPF =∠M =∠F =∠KNM

△MNK=△FPK (по стороне и прилежащим углам)

Объяснение:

Доказательство приведено в приложенном к ответу файле (рис. + пояснения)